摩尔投票法_多数元素(绝对众数)

[题目来源](408 时间复杂度为 O(n)、空间复杂度为 O(1) - 多数元素 - 力扣（LeetCode）)

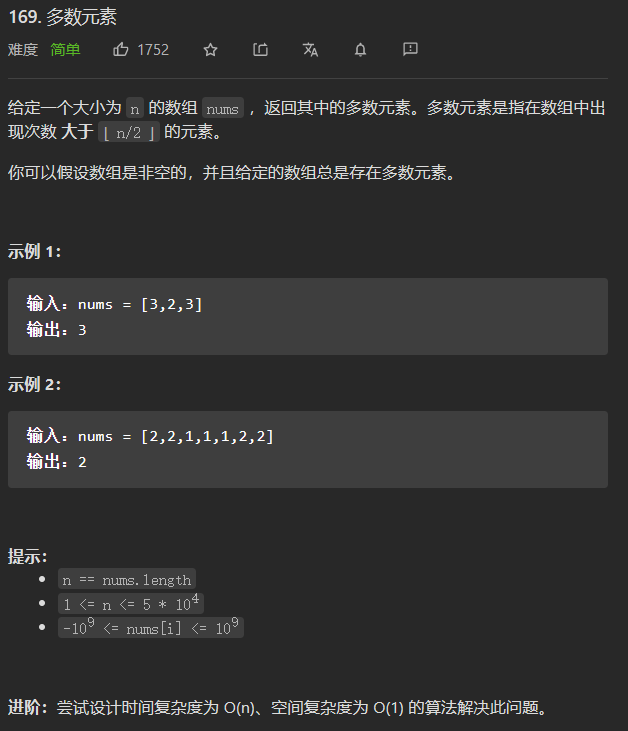
一般有以下三种思路：

暴力求解，从第一个元素开始记录，遇到与第一个元素值相同的元素就计数+1，当某个元素的个数大于等于n/2的时候，说明就是这个元素最多
先排序，后返回容器中第n/2个元素

摩尔投票法：

解决的问题是如何在任意多的候选人（选票无序），选出获得票数最多的那个。
（解决绝对众数的问题：如果一个元素出现的次数大于等于其他所有数出现的次数之和，那么这个数就是绝对众数，也就是说如n个数里如果有一个数的数量大于等于n/2，这个数就是绝对众数）
形象化描述：
想象着这样一个画面：
会议大厅站满了投票代表，每个都有一个牌子上面写着自己所选的候选人的名字。然后选举意见不合的（所选的候选人不同）两个人，会打一架，并且会同时击倒对方。显而易见，如果一个人拥有的选票比其它所有人加起来的选票还要多的话，这个候选人将会赢得这场“战争”，当混乱结束，最后剩下的那个代表（可能会有多个）将会来自多数人所站的阵营。
但是如果所有参加候选人的选票都不是大多数（选票都未超过一半），那么最后站在那的代表（一个人）并不能代表所有的选票的大多数。因此，当某人站到最后时，需要统计他所选的候选人的选票是否超过一半（包括倒下的），来判断选票结果是否有效。
在本题中，显然是一定有一个候选人的选票达到大半的
算法的描述：
我们维护一个 x ，表示当前的候选人，然后维护一个 num，用来表示当前候选人的选票数。对于每一张新的选票，如果它投给了当前的候选人，就把 num 加1，否则就把 num 减1（也许你可以想象成，B的一个狂热支持者去把A的一个支持者揍了一顿，然后两个人都没法投票）。特别地，计票过程中如果 num=0 ，我们可以认为目前谁都没有优势，所以新的选票投给谁，谁就成为新的候选人。
如果我们要求的是众数，这样的做法并不能给出正确答案，但如果要求的是绝对众数（且绝对众数确实存在），那么 n 一定是正确的。
这是因为，在最后计票时，我们知道有 num 张票投给了 x ，假如绝对众数另有其人，那么一定是剩下的票投出来的。但剩下的 x− num 张票都是在“捉对厮杀”的过程中被抵消掉的，每一对被抵消的票都来自不同的候选人，所以一个候选人最多在这里拿到 n−num/2 票，这不可能大于 n/2 。但绝对众数确实存在，所以这个绝对众数就一定是 m 。
如果绝对众数不存在，摩尔投票会给出一个错误的解，所以一定要记得验证答案。
算法的实现
1
2
3
4
5
6
7
8
9
10
11
int x = 0, num = 0;
for(int i = 0; i<n; i++)
{
    if(num = 0)
        x = A[i];
    if(A[i] == x)
        num++;
    else
        num--;
}
//如果实际情况下绝对众数本身就是不存在的，那么会得到一个错误的解，此时需要进行一下验证

摩尔投票法的进阶：

简单的摩尔投票法只是能找到一个选票最多的。但是如果要求选出N个人，这个N个人只要满足票数大于1/(N+1)就可以，也是可以摩尔投票法的思想，只是需要进行一下修改

int x[N], num[N];
for (auto e : nums) {
    int i = find(x, x + N, e) - x;
    if (i != N) { // 如果当前票投给了候选人之一
        num[i]++;
        continue;
    }
    int j = find(num, num + N, 0) - num;
    if (j != N) { // 如果当前存在一个位置"虚位以待"
        x[j] = e;
        num[j] = 1;
        continue;
    }
    for (auto &c : num)
        c--;
}
// 最后需要验证答案是否符合要求

原理是一样的。最后我们可以把票分为2个部分：投给了最多 N 个候选人的一部分，和被抵消的一部分。后者可以划分为若干个 N+1 元组，每个元组内的票都来自不同的候选人。因此，只有那些属于第一部分的人的票数可能超过总数的 1/(N+1) 。