数据结构_二叉树（C++实现

1前言：此类笔记仅用于个人复习，内容主要在于记录和体现个人理解，详细还请结合bite课件、录播、板书和代码。

[toc]

前言

  1. 本篇中的是一般二叉树(包括线索树、表达式树)是通过链式结构实现的，关于顺序结构的实现请见C语言版(顺便有堆的相关内容)
  2. 本篇中哈夫曼树的结点存储是用的是顺序结构
  3. 模版不支持分离编译，因此跟以往自定义变量和函数时，声明在头文件、实现在源文件不同，定义(声明+实现)都是在头文件中【详见code日记】

二叉树

采用链式存储

二叉树类的声明：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#pragma once

//模版不支持分离编译！！！

//二叉树的链式存储
#include <iostream>
#include <queue>
#include <stack>
#include <vector>
#include <sstream>//在buildExpressionTree中用到，用来进行string转等价int

using namespace std;

class nullPoint
{
};

//binaryTree类的向前说明
template<class elemType>
class binaryTree;

template<class elemType>
class Node//二叉树结点类
{
	friend class binaryTree<elemType>;//结点类将二叉树类视为友元函数

private:
	elemType data;
	Node<elemType> *left;//指针域
	Node<elemType> *right;
	int leftFlag; //用于标识孩子指针是否为线索，0则说明left指向该结点的左孩子，1则说明left指向该结点的直接前驱
	int rightFlag; //用于标识孩子指针是否为线索，0则说明right指向该结点的右孩子，1则说明right指向该结点的直接后继

public:
	Node()
	{
		left = NULL;
		right = NULL;
		leftFlag = 0;
		rightFlag = 0;
	}

	Node(const elemType& data, Node<elemType> *left = NULL, Node<elemType> *right = NULL)
	{
		this->data = data;
		this->left = left;
		this->right = right;
		leftFlag = 0;
		rightFlag = 0;
	}
};

template<class elemType>
class binaryTree//二叉树类
{
private:
	Node<elemType> *root;//链式二叉树的根结点指针
	elemType stopFlag;//结束标志

public:
	binaryTree()
	{
		root = NULL;
	}

	void creatTree(const elemType& flag);//创建一棵二叉树

	bool isEmpty()
	{
		return root == NULL;
	}

	Node<elemType> *getRoot()
	{
		return root;
	}

	int Size(Node<elemType> *t);//递归求二叉树的结点的个数
	int Size();//求二叉树的结点个数

	int Height(Node<elemType> *t);//递归求二叉树的高度/深度
	int Height();//求二叉树的高度

	void delTree(Node<elemType> *t);//递归删除二叉树
	void delTree();//删除二叉树

	void preOrder(Node<elemType> *t);//按前序遍历输出以t为根的二叉树的结点的数据值
	void preOrder();//前序遍历

	void inOrder(Node<elemType> *t);//按中序遍历输出以t为根的二叉树的结点的数据值
	void inOrder();//中序遍历

	void postOrder(Node<elemType> *t);//按后序遍历输出以t为根的二叉树的结点的数据值
	void postOrder();//后序遍历

	void levelOrder();//层序遍历

	Node<elemType> *threadMin();//建立中序遍历线索树
	void threadMidInOrder(Node<elemType> *first);//借助 在原二叉树基础上 建立的中序遍历线索树，对于原二叉树实现非递归的中序遍历
	void threadMidPreOrder();//借助 在原二叉树基础上 建立的中序遍历线索树，对于原二叉树实现非递归的前序遍历

	Node<elemType> *buildTree(elemType pre[], int pl, int pr,
		elemType mid[], int ml, int mr);//已知一颗二叉树的前序遍历和中序遍历结果 建立这颗二叉树
	//数组pre、mid分别是前序遍历、中序遍历的结果;pl、pr、ml、mr分别是前序、中序遍历结果数组的边界


	vector<string> init(const string& s);//先将string类型的表达式，将元素由char变成string并存在vector中
	// 这样才可以计算多位数
	int judge(const string& s);//判断操作符优先度
	int stringToInt(string s);//;string转成等价的int
	void buildExpressionTree(const string& s);//将当前树建立为表达式树
	int calculateExpressionTree();//计算当前这颗表达式树

};

二叉树类的成员变量介绍

二叉树结点类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//binaryTree类的向前说明
template<class elemType>
class binaryTree;

template<class elemType>
class Node//二叉树结点类
{
	friend class binaryTree<elemType>;//结点类将二叉树类视为友元函数

private:
	elemType data;
	Node<elemType> *left;//指针域
	Node<elemType> *right;
	int leftFlag; //用于标识孩子指针是否为线索，0则说明left指向该结点的左孩子，1则说明left指向该结点的直接前驱
	int rightFlag; //用于标识孩子指针是否为线索，0则说明right指向该结点的右孩子，1则说明right指向该结点的直接后继

public:
	Node()
	{
		left = NULL;
		right = NULL;
		leftFlag = 0;
		rightFlag = 0;
	}

	Node(const elemType& data, Node<elemType> *left = NULL, Node<elemType> *right = NULL)
	{
		this->data = data;
		this->left = left;
		this->right = right;
		leftFlag = 0;
		rightFlag = 0;
	}
};

data为结点的数据域

left和right是指针域

leftFlag/rightFlag用于标识 孩子指针是否为线索，0则说明孩子指针保存的是指向该结点的孩子的地址，1则说明孩子指针保存的是该结点的直接前驱/后继的地址

详见二叉线索树

二叉树类的成员变量

1
2
3
4
5
6
7
8
template<class elemType>
class binaryTree
{
private:
	Node<elemType> *root;//链式二叉树的根结点指针
	elemType stopFlag;//结束标志


stopFlag：在创建二叉树的时候，需要不断获取二叉树的结点，这个变量是用来 终止获取结点 的结束标志

二叉树类的实现：

二叉树的构建

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//模版不支持分离编译！！！
template<class elemType>
void binaryTree<elemType>::creatTree(const elemType& flag)//创建一棵二叉树
//借助队列来创建一颗二叉树
{
	queue<Node<elemType> *> que;
	elemType e, el, er;//根结点、左孩子、右孩子的data
	Node<elemType> *p, *pl, *pr;//根结点、左孩子、后孩子的地址

	stopFlag = flag;

	cout << "Please input the root:";//输入根结点的值
	cin >> e;

	if (e == flag)//判断是否为结束标志
	{
		root = NULL;
		return;
	}

	p = new Node<elemType>(e);//new一个Node结点，作为根结点
	root = p;

	que.push(p);

	while (!que.empty())
	{
		p = que.front();
		que.pop();//获得队首元素并出队

		cout << "Please input the left_child and the right_child of " << p->data << " using " << stopFlag
			 << " as no child";
		cin >> el >> er;

		if (el != stopFlag)//如果根结点有左孩子
		{
			pl = new Node<elemType>(el);
			p->left = pl;
			que.push(pl);
		}

		if (er != stopFlag)//如果根结点有右孩子
		{
			pr = new Node<elemType>(er);
			p->right = pr;
			que.push(pr);
		}
	}
}

借助队列构建二叉树

首先创建树的根结点入队列

只要队列不为空，循环

每次获取队首元素p并出队

若p有孩子，则创建p的左/右孩子结点，让p的指针域指向它们，并将左右孩子入队列。

否则不执行操作，进入下一次循环

队空，结束 截屏2022-11-17 13.11.05

递归求以二叉树的结点的个数

1
2
3
4
5
6
7
8
9
10
11
template<class elemType>
int binaryTree<elemType>::Size(Node<elemType> *t)//递归求二叉树的结点的个数
{
	return t == NULL ? 0 : 1 + Size(t->left) + Size(t->right);
}

template<class elemType>
int binaryTree<elemType>::Size()
{
	return Size(root);
}

可以结合图思考

image-20221014105348435

递归求二叉树的高度/深度

1
2
3
4
5
6
7
8
9
10
11
12
13
14
template<class elemType>
int binaryTree<elemType>::Height(Node<elemType> *t)//递归求二叉树的高度
{
	if (!t)
		return 0;
    
	return Height(t->left) > Height(t->right) ? Height(t->left) + 1 : Height(t->right) + 1;
}

template<class elemType>
int binaryTree<elemType>::Height()
{
	return Height(root);
}

节点的层次：从根开始定义，根为第一层，根的子结点所在的为第二层，以此类推

如下图，A的层次是1，C的是2，H的是4

树的高度/深度：根中结点的最大层次，下图中树的高度就是4

思路：递归

结点为空则返回高度为0，否则返回当前结点为根结点的树的高度：

左右子树比较高度，更高的高度+1，就是当前结点为根结点的树的高度

QQ图片20221117235938

递归删除二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
template<class elemType>
void binaryTree<elemType>::delTree(Node<elemType> *t)//递归删除二叉树
{
	if (!t)
		return;
	delTree(t->left);
	delTree(t->right);

	delete t;
	/*这里t不用指向NULL，1是因为它是形参，指向也没用，2是下面的root需要指向形参是因为root是类的成员函数，后续还会调用它
	避免root指向被释放的空间，造成非法访问，成为野指针*/
    
template<class elemType>
void binaryTree<elemType>::delTree()
{
	delTree(root);
	root = NULL;
}

二叉树的遍历：

二叉树的递归遍历：
前序遍历(递归)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
template<class elemType>
void binaryTree<elemType>::preOrder(Node<elemType> *t)//递归，按前序遍历输出以t为根的二叉树的结点的数据值
{
	if (!t)
	{
		//cout << "NUll ";//如果想要更清楚观察前序遍历的原理，可以在空结点时输出"NULL "
		return;
	}

	cout << t->data << " ";//根，左，右
	preOrder(t->left);
	preOrder(t->right);
}

//template<class elemType>
//void binaryTree<elemType>::preOrder()//递归，前序遍历整棵树
//{
//	preOrder(root);
//}
中序遍历(递归)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
template<class elemType>
void binaryTree<elemType>::inOrder(Node<elemType> *t)//递归，按中序遍历输出以t为根的二叉树的结点的数据值
{
	if (!t)
	{
		//cout << "NUll ";//如果想要更清楚观察前序遍历的原理，可以在空结点时输出"NULL "
		return;
	}

	inOrder(t->left);//左，根，右
	cout << t->data << " ";
	inOrder(t->right);
}

//template<class elemType>
//void binaryTree<elemType>::inOrder()//递归，中序遍历整棵树
//{
//	inOrder(root);
//}
后序遍历(递归)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
template<class elemType>
void binaryTree<elemType>::postOrder(Node<elemType> *t)//递归，按后序遍历输出以t为根的二叉树的结点的数据值
{
	if (!t)
	{
		//cout << "NUll ";//如果想要更清楚观察前序遍历的原理，可以在空结点时输出"NULL "
		return;
	}

	postOrder(t->left);
	postOrder(t->right);
	cout << t->data << " ";
}

//template<class elemType>
//void binaryTree<elemType>::postOrder()//递归，后序遍历整棵树
//{
//	postOrder(root);
//}
二叉树的非递归遍历：

二叉树的非递归遍历，需要用 栈 来进行辅助

前序遍历(非递归)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
template<class elemType>
void binaryTree<elemType>::preOrder()//非递归，前序遍历整棵树
{
	if (!root)
		throw nullPoint();

	Node<elemType> *p;//当前访问的结点
	stack<Node<elemType> *> s;//辅助栈，存放即将访问的结点

	s.push(root);
	while (!s.empty())
	{
		p = s.top();
		s.pop();

		cout << p->data << " ";

		if (p->right)
			s.push(p->right);
		if (p->left)
			s.push(p->left);
	}
	cout << endl;
}

前序遍历的访问是“根、左、右”

用一个栈s存储 需要遍历的结点 ，先将root入栈

只要栈不为空，就循环

获取栈顶元素p并出栈

访问p结点，输出p的data

看p有无左/右孩子，有则入栈

注意应让右孩子先入栈，再让左孩子入栈

因为栈的特性，后进先出，前序遍历要求访问完根结点之后先访问它的左孩子

所以应先让右孩子入栈，再让左孩子入栈，这样才能保证栈顶元素是左孩子

还是因为栈的特性，访问结点的时候让它的孩子入栈，这样就保证了访问完结点之后访问的就是它的孩子

QQ截图20221118113318
中序遍历(非递归)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
template<class elemType>
void binaryTree<elemType>::inOrder()//非递归，中序遍历整棵树
{
	if (!root)
		throw nullPoint();

	Node<elemType> *p;//当前结点
	stack<Node<elemType> *> s1;//辅助栈，保存即将访问的结点

	int flag;//用来记录结点的访问情况：是否访问过左孩子。没访问过则左孩子入栈；访问过左孩子才能访问当前结点的data，然后将右孩子入栈
	//未访问过左孩子，值为0，访问过左孩子，值为1
	stack<int> s2;//保存s1中每个结点的访问情况

	s1.push(root);
	s2.push(0);//root的初始访问情况是0

	while (!s1.empty())
	{
		p = s1.top();//获取栈顶元素，为当前结点
		flag = s2.top();//获取栈顶元素，为当前结点的访问情况

		if (flag == 1)//如果访问过当前结点的左孩子，则访问当前结点的data，输出data、右孩子入栈
		{
			
			cout << p->data << " ";//访问输出当前结点的data
  		//访问完了当前结点的data，当前结点应当出栈
      s1.pop();
			s2.pop();

			if (p->right)//有右孩子则压栈
			{
				s1.push(p->right);//右孩子压栈
				s2.push(0);//右孩子的初始访问情况是0
			}
		}
		else//没访问过左孩子
		{
			s2.pop();
			s2.push(1);//更新当前结点的访问情况

			if (p->left)//左孩子入栈
			{
				s1.push(p->left);
				s2.push(0);//左孩子初始访问情况是0
			}
		}
	}
	cout << endl;
}

中序遍历的访问顺序是“左、根、右”

在访问结点的时候，需要考虑该结点是否访问过左孩子，若没有访问左孩子，则应先访问左孩子，之后再访问当前结点data，然后再访问右孩子

用flag记录结点的访问情况，未访问过左孩子则值为0，访问过则值为1，根据flag来判断对当前结点如何操作

QQ截图20221118113318
后序遍历(非递归)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
template<class elemType>
void binaryTree<elemType>::postOrder()//非递归，后序遍历整棵树
{
	if (!root)
		throw nullPoint();

	Node<elemType> *p;//当前结点
	stack<Node<elemType> *> s1;//辅助栈，保存即将访问的结点

	int flag;//用来记录当前结点的访问情况。没访问过左孩子则左孩子入栈；访问过左孩子但没有访问过右孩子则右孩子入栈；访问过右孩子才能访问当前结点的data
	//未访问过左孩子，值为0；访问过左孩子未访问过右孩子，值为1；访问过右孩子，值为2
	stack<int> s2;//保存s1中每个结点的访问情况

	s1.push(root);
	s2.push(0);//root的初始访问情况是0

	while (!s1.empty())
	{
		p = s1.top();//获取栈顶元素，为当前结点
		flag = s2.top();//获取栈顶元素，为当前结点的访问情况

		if (flag == 2)//访问过当前结点的右孩子，则访问当前结点的data
		{
			cout << p->data << " ";//访问输出当前结点的data
  		//访问完了当前结点的data，当前结点应当出栈
      s1.pop();
			s2.pop();
		}

		else if (flag == 1)//访问过当前结点的左孩子但未访问右孩子
		{
			s2.pop();
			s2.push(2);//更新当前结点的访问情况

			if (p->right)//有右孩子则压栈
			{
				s1.push(p->right);
				s2.push(0);//右孩子的初始访问情况是0
			}
		}

		else if (flag == 0)//未访问过当前结点的左孩子
		{
			s2.pop();
			s2.push(1);//更新当前结点的访问情况

			if (p->left)//左孩子入栈
			{
				s1.push(p->left);
				s2.push(0);//左孩子初始访问情况是0
			}
		}
	}
	cout << endl;
}

思路跟中序遍历类似，访问结点的时候按照“左、右、根”的顺序

访问结点的时候要判断是否访问过左孩子，没有访问过左孩子要先访问左孩子，如果访问过左孩子要判断是否访问过右孩子，访问过右孩子才能访问当前结点，输出当前结点的值

flag为 0 说明 未访问过当前结点的左孩子；1则说明访问过左孩子但是没访问右孩子；2则说明访问过右孩子，可以输出当前结点的data

层序遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
template<class elemType>
void binaryTree<elemType>::levelOrder()//层序遍历
{
	queue<Node<elemType> *> que;//辅助队列保存即将访问的结点
	Node<elemType> *p;//当前访问的结点

	if (!root)
		throw nullPoint();

	que.push(root);
	while (!que.empty())
	{
		p = que.front();
		que.pop();
		cout << p->data << " ";

		if (p->left)
			que.push(p->left);

		if (p->right)
			que.push(p->right);
	}
	
	cout << endl;
}

二叉线索树：

对于n个结点的二叉树，在二叉链存储结构总中有n+1个空链域

有些结点没有左/右孩子，指针域保存的地址是空的，这个指针域是空链域

利用这些空链域存放在 某种遍历次序下的结果中 该结点的 直接前驱结点 和 直接后继结点 的指针，这些指针称为线索，加上线索的二叉树称为线索二叉树。

直接前驱、直接后继：通过某种遍历方式，获得二叉树的遍历结果，在遍历结果中，某个结点的前一个结点就是 在当前遍历方式下 自己的直接前驱，后一个结点就是 在当前遍历方式下 自己的直接后继

如果指针域的指针存的是直接前驱/后继的地址，则就能找到当前结点的直接前驱或者直接后继，这就为遍历提供了线索，故称这种指针为线索

根据线索性质的不同，二叉树可分为前序遍历线索二叉树、中序遍历线索二叉树和后序遍历线索二叉树三种。

中序遍历线索二叉树的构建
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
template<class elemType>
Node<elemType> *binaryTree<elemType>::threadMin()//建立中序遍历线索树
//实质就是在中序遍历的时候将结点的空链域存上线索
{
	if (!root)
		throw nullPoint();

	Node<elemType> *first = NULL;//记录中序遍历结果中的第一个结点
	Node<elemType> *pre = NULL;//在中序遍历中当前结点的直接前驱

	Node<elemType> *p;//当前结点
	stack<Node<elemType> *> s1;
	
	int flag;
  stack<int> s2;

	s1.push(root);
	s2.push(0);

  //实质就是在中序遍历的时候将结点的空链域存上线索
	while (!s1.empty())
	{
    p = s1.top();
		flag = s2.top();

		if (flag == 1)
		{
			cout << p->data << "-----" << endl;
      s1.pop();
      s2.pop();

			if (!first)//p结点data在此已经访问完了，如果first为空说明p就是中序遍历结果中的第一个结点
				first = p;

			if (p->right && p->rightFlag == 0)//如果当前结点有右孩子，右孩子入栈
        //rightFlag == 0说明右指针存的是右孩子，== 1说明右指针存的是直接后继
			{
				s1.push(p->right);
				s2.push(0);
			}

			if (!p->left)//如果左指针为空，用来存直接前驱
			{
				p->leftFlag = 1;
				p->left = pre;
        
//////////////辅助调试，输出一下当前结点直接前驱的data///////////////////////
				cout << p->data << "'s pre: ";
				if (p->left)
					cout << p->left->data << endl;
				else//中序遍历结果中的第一个结点没有直接前驱，是线索二叉树中唯一一个左指针为空的
					cout << "NULL" << endl;
///////////////////////////////////////////////////////////////////////
			}

			if (!p->right)//如果右指针为空，用来存直接后继
			{
				p->rightFlag = 1;
				p->right = !s1.empty() ? s1.top() : NULL;
        //s1栈顶就是当前结点的直接后继，如果栈为空，说明当前结点是中序遍历结果中的最后一个结点，是线索二叉树中唯一一个右指针为空的

//////////////辅助调试，输出一下当前结点直接前驱的data///////////////////////
				cout << p->data << "'s next: ";
				if (p->right)
					cout << p->right->data << endl;
				else//中序遍历结果中的最后一个结点没有直接后继，是线索二叉树中唯一一个右指针为空的
					cout << "NULL" << endl;
//////////////////////////////////////////////////////////////////////
			}

			pre = p;//已访问完当前结点，当前结点成为了下一个要访问的结点的直接前驱
		}

		else//如果flag == 0
		{
      s2.pop();
			s2.push(1);

			if (p->leftFlag == 0 && p->left)//左结点为左孩子的话，将左孩子入结点栈
			{
				s1.push(p->left);
				s2.push(0);
			}
		}

	}

	return first;
}

在进行中序遍历的时候顺便对当前访问的结点添加上线索

访问的上一个结点是当前结点的直接前驱，即将访问的下一个结点(栈顶元素)是当前结点的直接后继

借助中序遍历线索树实现 中序非递归遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
template<class elemType>
void binaryTree<elemType>::threadMidInOrder(Node<elemType> *first)//借助中序线索树，非递归 中序遍历原来的二叉树
{
	if (!first || !root)
		throw nullPoint();

	Node<elemType> *p = first;

	while (p)
	{
		cout << p->data << " ";

		if (p->rightFlag == 0)//如果p有右孩子，访问p的右孩子
		{
			p = p->right;

			while (p->leftFlag == 0 && p->left)//当前结点有左子树，应访问左子树的最左结点
				p = p->left;
		}
    
		else//如果p无右孩子，则直接用线索找它的直接后继
			p = p->right;
		
	}
	cout << endl;
}

从first开始遍历

遍历结点时

有右孩子去往右孩子，访问右孩子时，右孩子有左子树，则去往左子树的最左结点

无右孩子则去往直接后继

iShot_2022-11-20_10.41.22
借助中序遍历线索树实现 前序非递归遍历
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
template<class elemType>
void binaryTree<elemType>::threadMidPreOrder()//借助中序线索树，非递归 前序遍历 原来的二叉树
{
	if (!root)
		throw nullPoint();

	Node<elemType> *p = root;//从root开始访问

	while (p)
	{
		cout << p->data << " ";
		if (p->leftFlag == 0)//如果有左孩子，则直接访问左孩子
			p = p->left;

		else//没有左孩子则访问右孩子
		{
			while (p->rightFlag == 1 && p->right)//如果没有右孩子，则去往直接后继，直到有右孩子或者右结点为空(中序遍历结果中的最后一个结点
			{
				p = p->right;
			}

			p = p->right;//去往右孩子
		}
	}
	cout << endl;
}

从root开始遍历

有左孩子访问左孩子

没有左孩子访问右孩子，没有右孩子则去往直接后继，直到有右孩子，访问右孩子

已知前中序遍历结果，求二叉树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
template<class elemType>
Node<elemType> *binaryTree<elemType>::buildTree(elemType pre[], int pl, int pr,
	elemType mid[], int ml, int mr)//已知一颗二叉树的前序遍历和中序遍历结果 建立这颗二叉树
//数组pre、mid分别是前序遍历、中序遍历的结果;pl、pr、ml、mr分别是前序、中序遍历结果数组的边界
{
	Node<elemType> *p;//创建当前树的根结点
	Node<elemType> *leftRoot, *rightRoot;//创建当前树的左子树、右子树的根结点
	int i, pos, num;//pos：当前树的根在中序遍历中的位置，num：记录左子树结点个数
	//(根在前序遍历中的位置不用记录，前序遍历结果的第一个就是)
	int lpl, lpr, lml, lmr;//记录前序遍历、中序遍历中左子树的范围
	int rpl, rpr, rml, rmr;//记录前序遍历、中序遍历中右子树的范围

	if (pl > pr)
		return NULL;

	p = new Node<elemType>(pre[pl]);//创建当前树的根结点

	if (!root)
		root = p;//如果当前的二叉树是空树，那就直接让当前的树等于创建的二叉树

	for (i = ml; i <= mr; i++)//开始寻找前序遍历中的根在中序遍历中的位置
	{
		if (mid[i] == pre[pl])
			break;
	}
	pos = i;//----找到了中序遍历结果中的根结点----
	num = pos - ml;//记录左子树的结点个数

	lpl = pl + 1;//前序遍历结果中 左子树的范围
	lpr = pl + num;
	lml = ml;//中序遍历结果中 左子树的范围
	lmr = pos - 1;

	leftRoot = buildTree(pre, lpl, lpr, mid, lml, lmr);//递归，找遍历结果中 左子树中 的根结点

	rpl = lpl + 1;//前序遍历结果中 右子树的范围
	rpr = pr;
	rml = pos + 1;//中序遍历结果中 右子树的范围
	rmr = mr;

	rightRoot = buildTree(pre, rpl, rpr, mid, rml, rmr);//递归，找遍历结果中 右子树中 的根结点

	p->left = leftRoot;
	p->right = rightRoot;

	return p;
}

根据前序遍历“根、左、右”和中序遍历“左、根、右”

前序遍历结果中的第一个结点就是根，在中序遍历中找到这个根，中序遍历结果中这个根的左面的所有结点就是这个根的左子树的遍历结果，右面的所有结点就是右子树的遍历结果

这样可以用前序遍历结果找根，中序遍历结果找子树的遍历结果，构建完整二叉树

树是递归的结构，树可以分为根和子树，子树又分为根和子树

所以要递归找根结点，直到不能再分

例如：已知一棵树的前序遍历和中序遍历结果

前序序列：B、L、S、C、F、D、G、I、H

中序序列：L、S、B、F、C、I、G、H、D

理论思路过程：

image

算法实现：

pre、mid：前序遍历、中序遍历的结果结果数组

pl、pr、ml、mr：前序、中序遍历结果数组的左右边界

p：创建当前树的根结点

leftRoot、rightRoot：创建当前树的左子树、右子树的根结点
pos：记录当前树的根在中序遍历中的位置

(根在前序遍历中的位置不用记录，前序遍历结果的第一个就是)

num：记录左子树结点的个数

lpl、 lpr、 lml、 lmr：记录前序遍历、中序遍历中左子树的范围

rpl,、rpr,、rml、rmr：记录前序遍历、中序遍历中右子树的范围

​ iShot_2022-11-20_16.33.37

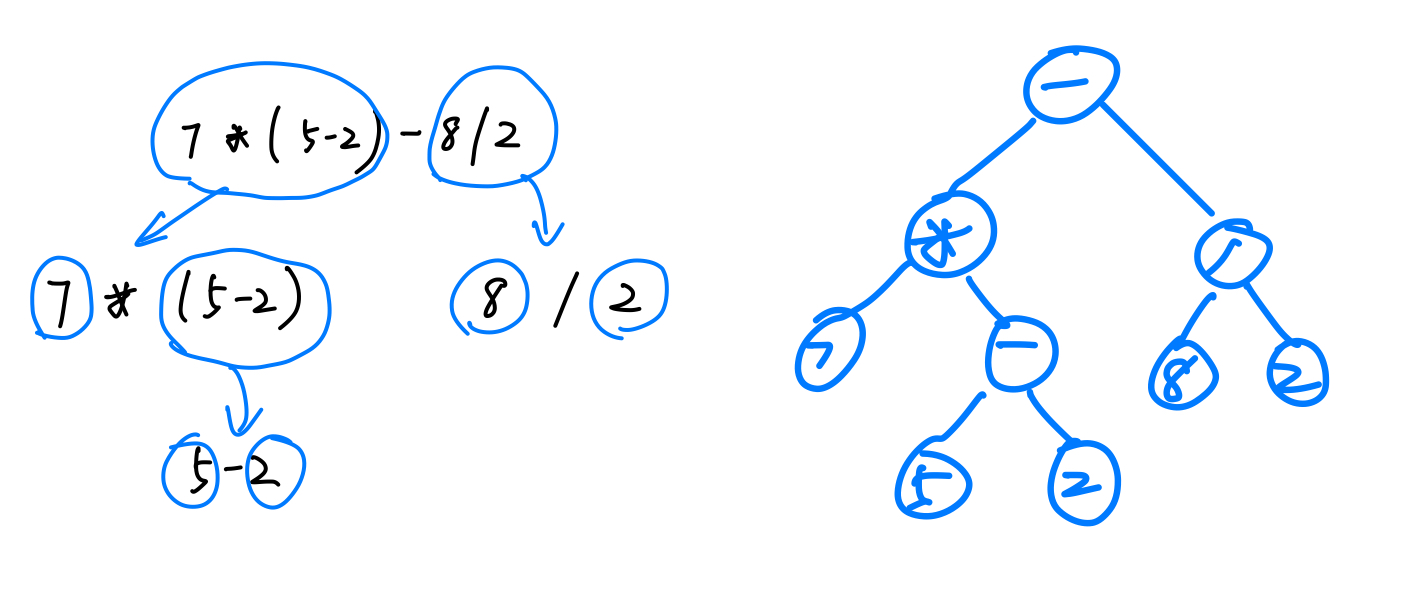
表达式树的构建：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
template<class elemType>
vector<string> binaryTree<elemType>::init(const string& s)//表达式的初始化处理
//原始表达式是string类型的，元素为char类型，因此值大于9的整数(也就是两位以上的整数)会被分成两个元素，无法正常表示和计算
//应先将表达式进行初始化：用元素类型为string的vector保存表达式的操作数和操作字符
{
	vector<string> v;
	int i = 0, j;

	while (i < s.length())
	{
		j = i;

		while (j < s.length() && s[j] <= '9' && s[j] >= '0')//如果遇到了数字，就往后看是否为多位数
		{
			j++;
		}

		if (i == j)//说明没有遇到数字
			v.push_back(s.substr(i++, 1));
		else
		{
			v.push_back(s.substr(i, j - i));
			i = j;
		}
	}

	return v;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
template<class elemType>
int binaryTree<elemType>::judge(const string& s)//判断操作符优先度
{
	if (s == "+" || s == "-")
		return 1;
	else if (s == "*" || s == "/")
		return 2;
	else if (s == "(")
		return 3;
	else if (s == ")")
		return -1;
	else
		return 0;
}
1
2
3
4
5
6
7
8
9
10
11
template<class elemType>
int binaryTree<elemType>::stringToInt(string s)//表达式中的操作数string类转int
{
	stringstream ss;
	int i;

	ss << s;
	ss >> i;

	return i;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
template<class elemType>
void binaryTree<elemType>::buildExpressionTree(const string& s)//将当前树建立为表达式树
{
	if (root)//表达式树应该用空树来建
	{
		cout << "This binaryTree is not a null tree , please define another binaryTree to make it as a ExpressionTree"
			 << endl;
		return;
	}

	stack<string> s1;//操作符栈
	stack<Node<string> *> s2;//子树栈，用来存放根结点的地址
	Node<string> *p, *left, *right;

	vector<string> v = init(s);//先将string类型的表达式初始化，将元素由char变成string并存在vector中

	for (int i = 0; i < v.size(); i++)
	{
		if (judge(v[i]) == 0)//如果是操作数，直接创建作为根结点进子树栈
		{
			p = new Node<string>(v[i]);
			s2.push(p);
		}

		else if (judge(v[i]) == 3)//如果当前操作符是左括号，直接进栈
			s1.push(v[i]);

		else if (judge(v[i]) == 1 || judge(v[i]) == 2)//如果是 加减乘除 操作符
		{
			if (s1.size() == 0)
				s1.push(v[i]);
			else
			{
				while (!s1.empty() && s1.top() != "(" && judge(v[i]) < judge(s1.top()))
					//如果栈不为空且栈顶元素不是"("，并且当前操作符优先度 小于栈顶，就让栈顶出栈
					//每次出栈，出栈的栈顶元素要与子树栈的两个栈顶元素构建成子树，并压入子树栈
				{

					right = s2.top();
					s2.pop();
					left = s2.top();
					s2.pop();//子树栈两个栈顶元素出栈

					p = new Node<string>(s1.top());
					s1.pop();//操作符栈顶元素出栈，与刚出子树栈的两个栈顶元素构建成子树，压入子树栈
					p->left = left;
					p->right = right;
					//在表达式树中，数字作为左结点是操作数，右结点是被操作数（表达式中左边的数是操作数，右边的数是被操作数
					//而表达式中的数字从左到右正序入栈，因此栈顶是被操作数，作为树结点的时候要记得反过来
					s2.push(p);
				}

				//当前操作符优先度不低于栈顶 or 栈为空
				s1.push(v[i]);
			}
		}

		else if (judge(v[i]) == -1)//当前操作符是右括号的话
		{
			while (judge(s1.top()) != 3)//在遇到左括号之前，一直将操作符栈顶弹栈
				//每次出栈，出栈的栈顶元素要与子树栈的两个栈顶元素构建成子树，并压入子树栈
			{
				right = s2.top();
				s2.pop();
				left = s2.top();
				s2.pop();

				p = new Node<string>(s1.top());
				s1.pop();
				p->left = left;
				p->right = right;

				s2.push(p);
			}

			s1.pop();//遇到左括号，左括号出栈
		}
	}

	while (!s1.empty())//处理操作符栈，将栈顶元素出栈直到栈空
		//每次出栈，出栈的栈顶元素要与子树栈的两个栈顶元素构建成子树，并压入子树栈
	{
		right = s2.top();
		s2.pop();
		left = s2.top();
		s2.pop();

		p = new Node<string>(s1.top());
		s1.pop();
		p->left = left;
		p->right = right;

		s2.push(p);

	}
	//子树栈中只会剩下一个根结点，这个根结点就是表达式树的根结点
	root = s2.top();
}

总体思路：

  1. 表达式其实是一种递归，表达式是由 左操作数 操作符 右操作数 组成

    而 操作数 是 表达式的值

    所以表达式 是由 左表达式的值 操作符 右表达式的值 组成

  2. 在计算表达式的时候，要先知道 左操作数 和 右操作数 才能进行计算，也就是要先计算左表达式和右表达式

  3. 在计算表达式的时候，优先度越高的表达式越先计算，其结果作为优先度低一级的部分的操作数

    因此表达式，是由优先度比自己高的表达式(的结果)组成的

  4. 所以表达式本质就是二叉树，左子树是左表达式，根结点是操作符，右子树是右表达式

    树的叶子结点是表达式里的操作数

IMG_0788

构建表达式树，就是优先度越高的部分组成的子树层次越深，越靠近叶子

从左到右顺序读取表达式的元素，将表达式的操作数都建成结点，这个是表达式树的叶子结点

优先级最高的表达式最先构建成树，并且成为优先级低于自己的表达式的子树

s1为操作符栈，用来比较操作符的优先度和存储操作符

s2为子树栈，存放已经建成的表达式子树

遍历表达式vector

如果是操作数，直接进s2栈

如果是操作符

  1. 如果s1栈为空，直接进s1

  2. 如果s1栈不为空

    1. 如果当前操作符为 左括号，直接进栈

    2. 如果当前操作符是 加减乘除，就与栈顶比较，如果栈顶不为空且不为 左括号，比栈顶优先级低，就让栈顶出栈，

      每次出栈，出栈的栈顶元素要与子树栈的两个栈顶元素构建成子树，并压入子树栈

    3. 如果当前操作符为 右括号，在遇到左括号之前，一直将操作符栈顶弹栈(操作符弹栈，按照👆的规矩)，直到遇到左括号，将左括号出栈

      每次出栈，出栈的栈顶元素要与子树栈的两个栈顶元素构建成子树，并压入子树栈

遍历完表达式之后，处理子树栈，将各个子树组成一个表达式树

将操作符栈栈顶出栈直到栈空，每次出栈，出栈的栈顶元素要与子树栈的两个栈顶元素构建成子树，并压入子树栈

子树栈中只会剩下一个根结点，这个根结点就是表达式树的根结点

表达式树的计算：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
template<class elemType>
int binaryTree<elemType>::calculateExpressionTree()//计算表达式树
//表达式数字都是叶子结点，操作符都是分支结点。用后序遍历访问整棵树，遇到数字就进操作数栈，遇到操作符就用操作数栈里的数字计算，结果入栈
//在后序非递归遍历的基础上进行修改即可
{
	if (!root)
		throw nullPoint();

	stack<Node<elemType> *> s1;
	stack<int> s2;
	Node<elemType> *p;
	int flag;//

	stack<int> num;//操作数栈

	s1.push(root);
	s2.push(0);

	while (!s1.empty())
	{
		flag = s2.top();
		s2.pop();
		p = s1.top();

		if (flag == 2)
		{
			s1.pop();

			if (p->data == "+" || p->data == "-" || p->data == "*" || p->data == "/")//如果是操作符，执行计算
			{
				int n2 = num.top();
				num.pop();
				int n1 = num.top();
				num.pop();

				if (p->data == "+")
					num.push(n1 + n2);
				else if (p->data == "-")
					num.push(n1 - n2);
				else if (p->data == "/")
					num.push(n1 / n2);
				else if (p->data == "*")
					num.push(n1 * n2);
			}

			else
			{
				num.push(stringToInt(p->data));//如果是操作数，转化为int之后存入操作数栈
			}

		}

		else if (flag == 1)
		{
			s2.push(2);

			if (p->right)
			{
				s1.push(p->right);
				s2.push(0);
			}
		}

		else if (flag == 0)
		{
			s2.push(1);

			if (p->left)
			{
				s1.push(p->left);
				s2.push(0);
			}
		}
	}
	return num.top();
}

计算的时候就采用后序遍历

访问当前结点之前先访问左右孩子，因此树中最先访问的是叶子结点也就是操作数，凡是操作数都入栈保存下来，在访问到操作符的时候就用栈中的操作数进行计算，计算结果作为操作数入栈

哈夫曼树/最优二叉树

路径：一个结点到另一个结点之间的通路就是路径。比如B到H就是一条路径，B到G也是一条路径

路径的长度：路径上经过的边(“树枝”)的数目。从根结点到第i层结点的路径的长度就是 i-1

结点的权：给一个结点赋予一个权值。比如给E一个权值20

结点的带权路径长度：根结点到一个带权结点的路径长度乘这个结点的权值。H的带权路径长度是2*19=38

树的带权路径长度(WPL)：所有叶子结点的带权路径长度之和。这棵树的WPL是2 * 44 + 3 * 19 + 2 * 46 + 2 * 11 = 259

截屏2022-11-21 16.23.38

哈夫曼树/最优二叉树：当有n的带权结点，都作为叶子结点构建成一棵二叉树时，如果构建成的二叉树的WPL最小，就称为“最优二叉树”，也称“哈夫曼树”

哈夫曼编码：在一棵哈夫曼树中，从根结点开始向下走，经过左孩子记为0，经过右孩子记为1，直到某个叶子结点，从根到这个叶子结点得到的0、1序列就是这个叶子结点的哈夫曼编码。比如，假设上面的树是哈夫曼树，H的哈夫曼编码求法：从A开始到H，A->B:0, B->E:1, E->H:1，叶子结点E的哈夫曼编码就是011.

哈夫曼树类的声明：

采用顺序存储

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include<iostream>
#include<vector>
#include <stack>

using namespace std;

//模版不支持分离编译！！！
template<class elemType>
class HFNode//构建哈夫曼树的结点
{
public:
	elemType data;
	double weight;
	int parents, left, right;//保存当前结点的父亲和孩子的位置下标

	HFNode()
	{
		weight = 0;
		parents = 0;
		left = 0;
		right = 0;
	}
};

template<class elemType>
class huffmanTree
{
private:
	HFNode<elemType> *HFTree;//哈夫曼树顺序表，其实这里用vector更方便一点
	int leafSize;//保存哈夫曼树叶子结点的个数
	vector<string> HFCode;//哈夫曼树编码表，保存每个叶子结点的哈夫曼编码
public:
	huffmanTree()
	{
		HFTree = NULL;
		leafSize = 0;
	}

	vector<HFNode<elemType>> getNode();//获取叶子结点集合
	void buildBestBinaryTree(vector<HFNode<elemType>> allNode);//创建最优二叉树/哈夫曼树

	HFNode<elemType> *getRoot()//返回构建好的哈夫曼树表的地址
	{
		return HFTree;
	}

	void makeHuffmanCode();//创建每个叶子结点的哈夫曼编码
};

哈夫曼树类的成员变量介绍

哈夫曼树结点类

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
template<class elemType>
class HFNode//构建哈夫曼树的结点
{
public:
	elemType data;
	double weight;
	int parents, left, right;//保存当前结点的父亲和孩子的位置下标

	HFNode()
	{
		weight = 0;
		parents = 0;
		left = 0;
		right = 0;
	}
};

相比普通二叉树的结点，由于用顺序表存储，孩子结点指针域换成了位置下标，并加了父结点位置下标

增加了结点的权值weight

哈夫曼树类的成员变量

1
2
3
4
5
6
7
template<class elemType>
class huffmanTree
{
private:
	HFNode<elemType> *HFTree;//哈夫曼树顺序表，其实这里用vector更方便一点
	int leafSize;//保存哈夫曼树叶子结点的个数
	vector<string> HFCode;//哈夫曼树编码表，保存每个叶子结点的哈夫曼编码

哈夫曼树类的实现：

哈夫曼树的构建

要想构建二叉树首先得有叶子结点，要先获取叶子结点集合

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
//模版不支持分离编译！！！
template<class elemType>
vector<HFNode<elemType>> huffmanTree<elemType>::getNode()//获取叶子结点集合
{
	vector<HFNode<elemType>> allNode;//创建一个容器，存储叶子结点

	cout << "Input the data and weight of the HFNode to add it " << endl;
	cout << "Before you input , input Y to continue ,or others to exit " << endl;
	char x;
	cin >> x;
	while (x == 'Y')
	{
		elemType data;
		double weight;
		cout << "input the data of the HFNode" << endl;
		cin >> data;
		cout << "input the weight of the HFNode" << endl;
		cin >> weight;

		HFNode<elemType> n;
		n.weight = weight;
		n.data = data;

		allNode.push_back(n);

		cout << "Input the data and weight of the HFNode to add it " << endl;
		cout << "Before you input , input Y to continue ,or others to exit " << endl;
		cin >> x;
	}
	leafSize = allNode.size();//当前存储的结点就是是之后建成的哈夫曼树的叶子结点
	return allNode;
}

用叶子结点集合构建哈夫曼树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
template<class elemType>
void huffmanTree<elemType>::buildBestBinaryTree(vector<HFNode<elemType>> allNode)//建立最优二叉树/哈夫曼树
{
	HFTree = new HFNode<elemType>[2 * allNode.size()];//构建哈夫曼树顺序表
	//按照最优二叉树的要求，初始带权值的结点都是叶子结点，也就是allNode里存储的都是叶子节点
	//并且根据最优二叉树的特点，会发现分支结点全部都是度为2的结点
	//根据二叉树的性质，叶子结点个数为n个，则度为2的结点个数为n-1
	//根据最优二叉树的构造方法，分支结点都是度为2的，因此最优二叉树中结点个数总是为2*n-1
	//我们开辟2*n个空间，空出第一个位置，如果表中的结点无父亲或孩子，那么就让对应的位置下标为0
	for (int i = 0; i < allNode.size(); i++)//叶子结点转移到哈夫曼树顺序表，并空出哈夫曼树表的第一个位置
	{
		HFTree[i + 1] = allNode[i];
		HFTree[i + 1].parents = 0;
		HFTree[i + 1].left = 0;
		HFTree[i + 1].right = 0;//一开始所有的结点都没有父亲和孩子
	}

	int i = allNode.size();//用i来表示当前没有父结点的结点的个数
	int n = allNode.size();//用n来表示当前哈夫曼树表中结点的个数，同时也算是最后面的元素的权重

	while (i != 1)//一开始所有结点都没有父结点，当哈夫曼树建立完成之后，只有根结点是没有父亲的，由此来判定哈夫曼树是否建成
		//由于每次循环创建一个新结点，原来权重最小的两个结点有了父结点，i-2，但是新结点是没有父结点的，所以每次循环总体上为i-1
		//(当然，也可以用n来判定循环，n<2*allNode.size()，画图理解即可）
	{
		int first_min, second_min;//定义没有父结点的结点中权重最小的两个结点的下标
		double first_min_weight = 9999;//将两个权重初始化为一个大到不可能的权重
		double second_min_weight = 9999;

		for (int x = 1; x <= n; x++)//寻找权重第一小的无父结点的结点
		{
			if (HFTree[x].parents == 0 && HFTree[x].weight < first_min_weight)
			{
				first_min = x;
				first_min_weight = HFTree[x].weight;
			}
		}
		for (int x = 1; x <= n; x++)//寻找权重第二小的无父结点的结点
		{
			if (x != first_min && HFTree[x].parents == 0 && HFTree[x].weight < second_min_weight)
			{
				second_min = x;
				second_min_weight = HFTree[x].weight;
			}
		}

		double weight_added = first_min_weight + second_min_weight;

		n++;

		HFTree[first_min].parents = n;//原来的权重最小结点变成了新结点的孩子
		HFTree[second_min].parents = n;

		HFTree[n].left = first_min;
		HFTree[n].right = second_min;
		HFTree[n].weight = weight_added;
		i--;//由于创建了一个新结点，原来权重最小的两个结点有了父结点，i-2，但是新结点是没有父结点的，所以总体上为i-1
	}

	//以下辅助调试代码，便于判断是否正确建立了一棵哈夫曼树
	for (int x = 1; x <= n; x++)
	{
		cout << "---------" << endl;
		cout << "index: " << x << endl;
		cout << "data: " << HFTree[x].data << endl;
		cout << "weight: " << HFTree[x].weight << endl;
		cout << "parents: " << HFTree[x].parents << endl;
		cout << "left: " << HFTree[x].left << endl;
		cout << "right: " << HFTree[x].right << endl;
		cout << "---------" << endl;
	}
}

哈夫曼算法：

每次找哈夫曼顺序表里权重最小的两个结点，创建一个新结点，新结点是权重是两个最小结点的和，最小结点是新结点的左孩子，次小结点是新结点的右孩子，新结点存入哈夫曼顺序表。这样构建出来的树就是哈夫曼树。

创建一个哈夫曼树顺序表用来存储哈夫曼树。

之前获得的叶子结点集合作为哈夫曼树的叶子结点。根据二叉树的性质，如果叶子结点的数目是n，则度为2的结点数目是n-1，而通过哈夫曼算法建立的哈夫曼树，所有的分支结点的度都是2，故哈夫曼树的结点总数是2n-1。

我们创建一个大小为2n的哈夫曼树顺序表，空出第一个位置，如果表中的结点无父亲或孩子，那么就让对应的下标为0

先将所有叶子结点添加到哈夫曼树表

刚开始所有的叶子结点都没有父亲、孩子，故父亲、孩子下标都为0

一开始所有结点都没有父结点，当哈夫曼树建立完成之后，只有根结点是没有父亲的，由此来判定哈夫曼树是否建成

由于每次循环创建一个新结点，原来权重最小的两个结点有了父结点，没有父结点的结点总数-2，但是新结点是没有父结点的，所以每次循环总体上为无父结点的结点总数-1

img

创建哈夫曼编码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

template<class elemType>
void huffmanTree<elemType>::makeHuffmanCode()//创建每个叶子结点的哈夫曼编码
//因为哈夫曼树顺序表里面前面的都是叶子结点(前半部分结点都是叶子结点，即(哈夫曼树顺序表结点个数+1)/2个）
//但是并没有写求哈夫曼树顺序表结点个数的函数，不过有记录叶子结点个数的变量leafSize
{
	stack<char> s;//每次用来存储单个叶子结点的编码

	HFCode.push_back(" ");//因为哈夫曼树表第一个元素没有存结点，这里保持和哈夫曼树表同步
	for (int i = 1; i <= leafSize; i++)//因为一共leafSize个结点，且是从权重1开始遍历，所以要遍历到第leafSize个，应该取到leafSize
	{
		int j = i;
		while (HFTree[j].parents != 0)//不断向上寻找当前结点的父亲，并且判断当前结点是其父亲的左孩子还是右孩子，左为'0'，右为'1'
		{
			if (HFTree[HFTree[j].parents].left == j)
				s.push('0');
			else
				s.push('1');

			j = HFTree[j].parents;
		}

		while (!s.empty())
		{
			HFCode[i].push_back(s.top());
			s.pop();
		}
	}

	//进行辅助调试
	for (int i = 1; i <= leafSize; i++)////因为一共leafSize个结点，且是从权重1开始遍历，所以要遍历到第leafSize个，应该取到leafSize
	{
		cout << "data is: " << HFTree[i].data << "  ";
		cout << "code is: " << HFCode[i] << endl;
	}
}

对于每一个叶子结点进行哈夫曼编码的时候，用字符栈保存自己的哈夫曼编码

不断向上寻找当前结点的父亲，并且判断当前结点是其父亲的左孩子还是右孩子，左为’0’，右为’1’

所有叶子结点的哈夫曼编码保存到HFCode中

结束

That’s all, thanks for reading!💐