数据结构_栈和队列_作业

2022.10.10智慧树作业_栈和队列

[toc]

第一题

相同点：

在逻辑上都是线性结构，栈和队列本质就是特殊的线性表，都可以用链表或者顺序表进行存储

不同点：

栈、队列具有特定的性质，特定的运算规则

第二题

1 2 3 4 5、1 2 3 5 4、1 2 4 3 5、1 2 4 5 3、1 2 5 4 3、1 3 2 4 5、1 3 2 5 4、1 3 4 2 5、1 3 4 5 2、1 3 5 4 2、1 4 3 2 5、1 4 3 5 2、1 4 5 3 2、1 5 4 3 2、2 1 3 4 5、2 1 3 5 4、2 1 4 3 5、2 1 4 5 3、2 1 5 4 3、2 3 1 4 5、2 3 1 5 4、2 3 4 1 5、2 3 4 5 1、2 3 5 4 1、2 4 3 1 5、2 4 3 5 1、2 4 5 3 1、2 5 4 3 1、3 2 1 4 5、3 2 1 5 4、3 2 4 1 5、3 2 4 5 1、3 2 5 4 1、3 4 2 1 5、3 4 2 5 1、3 4 5 2 1、3 5 4 2 1、4 3 2 1 5、4 3 2 5 1、4 3 5 2 1、4 5 3 2 1、5 4 3 2 1

第三题

现有一个元素均为整数的栈，使用另一个临时栈对其进行非递减排序

template <class elemType>
void seqStack<elemType>::sort()
{
    seqStack tmp;

    for (int k = Top; k > -1; k--)
    {
        int K = top();
        pop();

        if (tmp.isEmpty())
        {
            tmp.push(K);
        }
        else
        {
            while (!tmp.isEmpty())
            {
                if (K <= tmp.top())
                {
                    push(tmp.top());
                    tmp.pop();
                }
                else
                    break;
            }
            tmp.push(K);
            int q = Top;
            while (q >= k)
            {
                tmp.push(top());
                pop();
                q--;
            }
        }
    }
    while (!tmp.isEmpty())
    {
        push(tmp.top());
        tmp.pop();
    }
}

要求对栈进行非递减排序，就是栈底最大，栈顶最小

思路就是把主栈元素依次出到临时栈来进行排序，在临时栈中排成栈底最小，栈顶最大

主栈栈顶大于等于临时栈顶，直接出主栈入临时栈

小于临时栈顶，主栈栈顶先出栈赋值给k，临时栈逐个出栈到主栈，直到临时栈顶小于k，k入临时栈，在将之前放到主栈的临时栈元素放回临时栈

第四题

设计算法判别表达式中的括号是否配对出现， 平衡的表达式中’{‘、’}’，’(‘、’)’，’[‘、’]’ 应成对按序出现。

例如”{[()]{()}{()()}}” 是括号匹配的表达式， 而”[({}])”是括号不匹配的表达式

template <class elemType>
int seqStack<elemType>::parentheses(string s)
{
     int size = s.length();
    for (int x = 0; x < size; x++)
    {
        if (s[x] == '(' || s[x] == '{' || s[x] == '[')
        {
            push(s[x]);
        }
        else if (s[x] == ')' || s[x] == '}' || s[x] == ']')
        {
            if (s[x] == ')' && top() == '(')
                pop();
            else if (s[x] == '}' && top() == '{')
                pop();
            else if (s[x] == ']' && top() == '[')
                pop();
            else
                return -1;
        }
    }
    if (!isEmpty())
        return -1;

    return 0;
}

第五题

用两个栈实现队列

template <class elemType>
class Queue_stack
{
private:
    seqStack<elemType> a, b;

public:
    void push(const elemType &x)
    {
        b.push(x);
    }
    void pop()
    {
        if (a.isEmpty())
            while (!b.isEmpty())
            {
                a.push(b.top());
                b.pop();
            }
        a.pop();
    }
    elemType top()
    {
        if (a.isEmpty())
            while (!b.isEmpty())
            {
                a.push(b.top());
                b.pop();
            }
        return a.top();
    }
    void isEmpty()
    {
        return (a.isEmpty() && b.isEmpty());
    }
};

原理：一个栈负责入队列，一个栈负责出队列，一旦出队列栈为空，就把入队列栈中所有元素都出到出队列栈

第六题

用两个队列实现栈

#include "queue.cpp"

//用两个队列实现栈
template <class elemType> //先写一个求队列元素个数的函数，后面会用
int Queue<elemType>::size()
{
    Node<elemType> *p = head;
    int x = 0;
    while (p)
    {
        x++;
        p = p->next;
    }
    return x;
}

template <class elemType>
class Stack_queue
{
private:
    Queue<elemType> a, b;

public:
    void push(const elemType &x)
    {
        if (!a.isEmpty())
            a.pushQueue(x);
        else
            b.pushQueue(x);
    }
    void pop()
    {
        // assert(!a.isEmpty() && !b.isEmpty());
        Queue<elemType> *qEmpty = a.isEmpty() ? &a : &b;
        Queue<elemType> *qUnEmpty = a.isEmpty() ? &b : &a;
        while (qUnEmpty->size() > 1)
        {
            qEmpty->pushQueue(qUnEmpty->getHead());
            qUnEmpty->popQueue();
        }
        qUnEmpty->popQueue();
    }
    elemType top()
    {
        // assert(a.isEmpty() && !b.isEmpty());
        Queue<elemType> *qEmpty = a.isEmpty() ? &a : &b;
        Queue<elemType> *qUnEmpty = a.isEmpty() ? &b : &a;
        while (qUnEmpty->size() > 1)
        {
            qEmpty->pushQueue(qUnEmpty->getHead());
            qUnEmpty->popQueue();
        }
        int x = qUnEmpty->getHead();
        qEmpty->pushQueue(qUnEmpty->getHead());
        qUnEmpty->popQueue();
        return x;
    }
};

两个队列，一个总是空的，一个总是不空的

入栈就进非空队列，出栈把非空队列的前n个出到空队列，pop非空队列最后一个元素

非空队列就变成了空队列，空队列就变成了非队列

第七题

现有一个整数队列， 需要将其前 k 个元素进行逆置， 剩余的元素保持原来的顺序。
例如队列[1， 2， 3， 4， 5， 6， 7， 8， 9]， 若 k 为 4， 则需要将队列调整为[4， 3， 2， 1， 5，6， 7， 8， 9]

template <class elemType>
void Queue<elemType>::Reverse_k(int k)
{
    Queue<elemType> q;
    seqStack<elemType> s;

    int i=0;
    while(i<k)//前k个元素放到栈中
    {
        s.push(getHead());
        popQueue();
        i++;
    }
    while(head)//后n-k个元素放到临时队列中
    {
        q.pushQueue(getHead());
        popQueue();
    }

    while(!s.isEmpty())//栈中的元素放到主队列
    {
        pushQueue(s.top());
        s.pop();
    }
    while(q.head!=NULL)//临时队列的元素放到主队列中
    {
        pushQueue(q.getHead());
        q.popQueue();
    }
}

思路：前k个元素放到临时栈，后n-k个元素放到临时队列，再从临时栈中入到主栈，临时队列入到主栈

第八题

给定一个整型的顺序表， 表示在同一行的行星。 对于其中的元素， 正负值代表其一维的移动方向， 可以理解为正数代表行星向右移动， 负数代表行星向左移动。 方向相同的行星不会碰撞， 如果两个行星相向而行则会相互碰撞， 则较小的行星（绝对值代表行星大小）会爆炸， 大小相同时两者都会爆炸。 请设计程序给出行星碰撞后的结果。
例如： [4， 5， -3]， 5 与-3 发生碰撞， -3 爆炸而 5 幸存， 再没有负数即向左运动行星，碰撞结束结果为[4， 5]； [7， 1， -7]， 1 与-7碰撞， 1 爆炸而-7 幸存， 7 再与-7 碰撞， 两者都爆炸， 结果为[]。 注意如果是[-1,1]， 由于-1 向左而 1 向右， 两者不会碰撞。

template <class elemType>
void seqStack<elemType>::planet()
{
    seqStack<int> s;
    while (!isEmpty())
    {
        if (s.isEmpty())
        {
            s.push(top());
            pop();
        }
        else
        {
            if (s.top() < 0)
            {
                if (top() < 0)
                {
                    s.push(top());
                    pop();
                }
                else
                {
                    if (s.top() + top() > 0)
                        s.pop();
                    else if (s.top() + top() < 0)
                        pop();
                    else
                    {
                        s.pop();
                        pop();
                    }
                }
            }
            else
            {
                s.push(top());
                pop();
            }
        }
    }
    while (!s.isEmpty())
    {
        push(s.top());
        s.pop();
    }

}

思路：（有点 类似中缀式转后缀式）

这个顺序表就是主栈，再创建一个临时栈

临时栈为空，主栈栈顶进临时栈；主栈栈顶是小于0的，进临时栈；主栈栈顶大于0，临时栈小于零，判断他俩的和，大于零说明主栈栈顶绝对值大，保留主栈栈顶，临时栈顶出栈，否则反之，如果和等0，则两边都出栈。最后主栈空了就临时栈出栈到主栈

因为结果保存在了栈里，输出的时候顺序是反的，不过只要再写一个逆置的函数就可以，比如把栈元素放到队列了，再出队列到栈就可以了

第九题

现在有一批同学需要接收面试， 参加面试的同学按照先到先面试的原则接受面试官的考查。 本次面试中面试官最看重的是同学的成绩， 现在面试官小明需要你设计程序实现以下功能：
（1） 某位同学加入面试队伍， 输入其名字和成绩；
（2） 队伍最前端的同学的面试结束， 离开场地；
（3） 小明想知道当前面试队伍里最好成绩是多少。

template <class elemType>
class interview_team; //类的向前声明

template <class elemType>
class iNode
{
    friend class interview_team<elemType>; //看作Node的友元类,友元类可以访问Node的私有成员

private:
    string name;
    int point;
    iNode<elemType> *next;

public:
    iNode(string name = "null", int point = 0)
    {
        this->name = name;
        this->point = point;
        next = NULL;
    }
};

template <class elemType>
class interview_team
{
private:
    iNode<elemType> *head, *tail;

public:
    interview_team() { head = tail = NULL; }

    void i_push(string name, int point)
    {
        if (head == NULL)
        {
            head = tail = new iNode<elemType>(name, point);
        }
        else
        {
            tail->next = new iNode<elemType>(name, point);
            tail = tail->next;
        }
    }

    void i_pop()
    {
        if (head == NULL)
            return;

        iNode<elemType> *p = head;
        head = head->next;
        delete (p);

        if (head == NULL)
            tail == NULL;
    }

    int i_best()
    {
        if (!head)
            return -1;

        iNode<elemType> *p = head;
        int best = -1;

        while (p)
        {
            if (p->point > best)
                best = p->point;
            p = p->next;
        }

        return best;
    }
};

思路：其实就是实现STL的队列中的部分功能

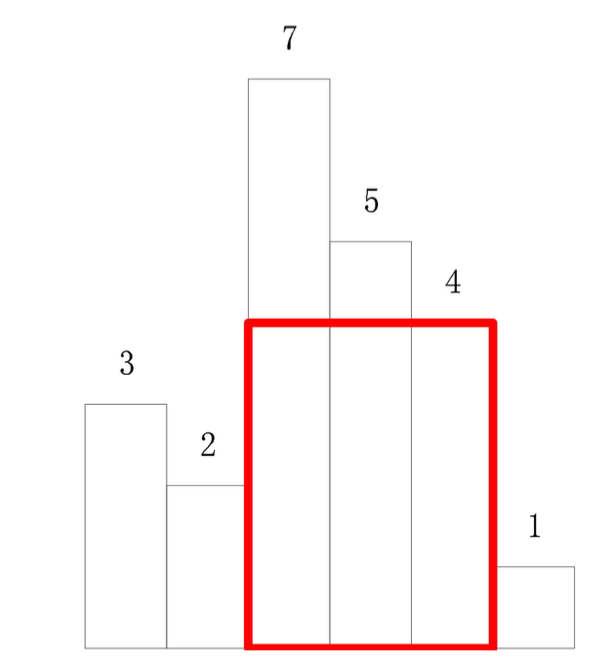
第十题

现有一个柱状图中，其中每个矩形柱子皆为相邻，且宽度相等，默认为 1，现在需要知道在这个柱形图中能够找到的最大矩形的面积。数据用一组非负的整数来表示，代表每根柱形的高度，请算出最大矩形的面积。

例如，已知每根柱形的宽度为 1，若给出的非负整数为[3,2,7,5,4,1]。图中的阴影部分为 最大矩形的面积，即 12 个单位的面积。

int Rectangle(seqStack<int> now)
{
    seqStack<int> pass;
    seqStack<int> elem;
    int rectangle = 0;
    while (!now.isEmpty())
    {
        int d = now.top();
        int p = 0;
        int n = 0;

        now.pop();
        elem.push(d);

        while (!pass.isEmpty())
        {
            if (pass.top() >= d)
            {
                elem.push(pass.top());
                pass.pop();
                p++;
            }
            else
                break;
        }
        while (!now.isEmpty())
        {
            if (now.top() >= d)
            {
                elem.push(now.top());
                now.pop();
                n++;
            }
            else
                break;
        }

        int r = d * (1 + p + n);
        if (r > rectangle)
            rectangle = r;

        while (n > 0)
        {
            now.push(elem.top());
            elem.pop();
            n--;
        }
        while (!elem.isEmpty())
        {
            pass.push(elem.top());
            elem.pop();
        }
    }
    return rectangle;
}

用栈

一个现在栈now（也是形参）

开两个临时站”临时站elem“、”过去栈pass“

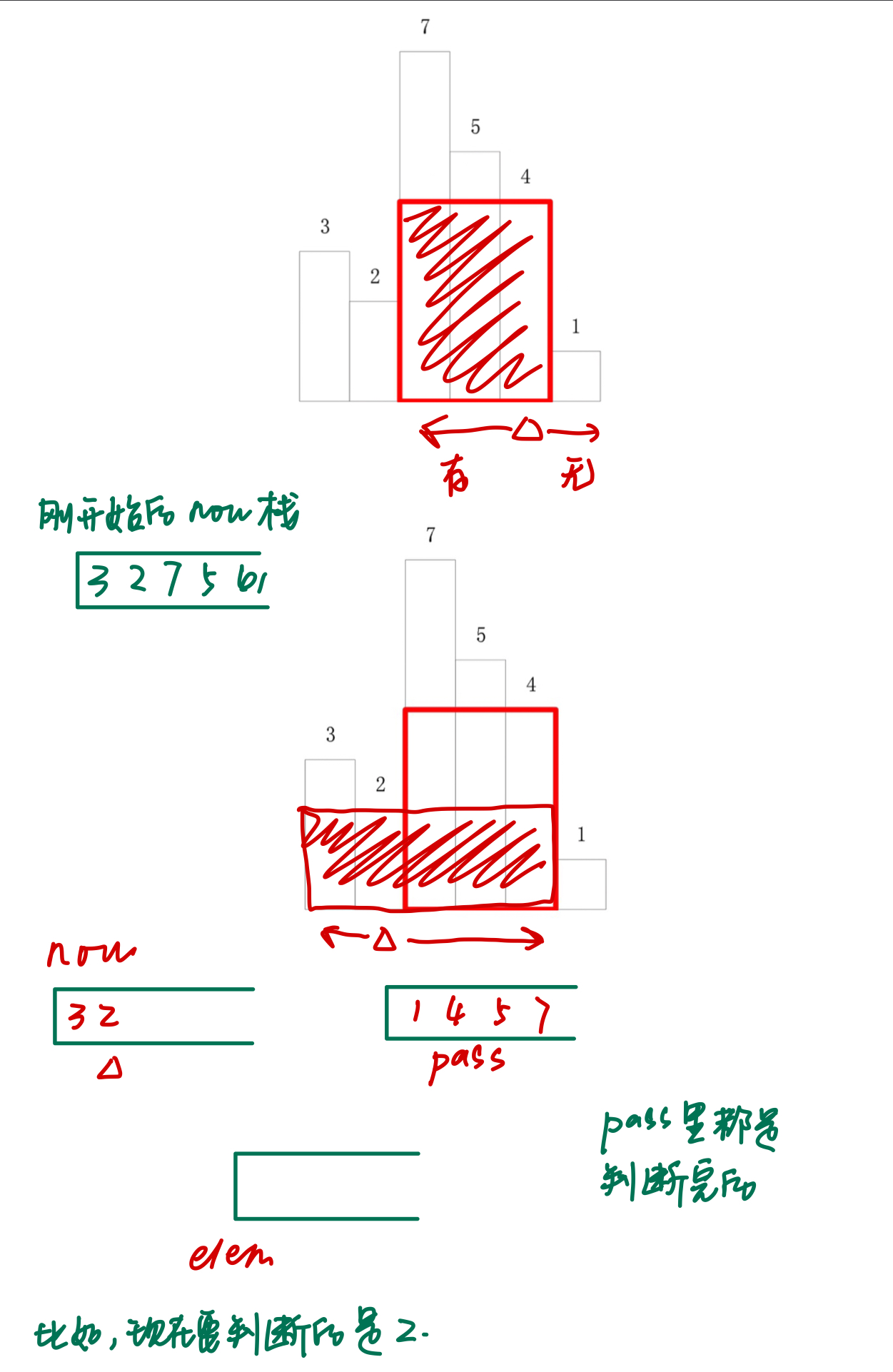
如果判断一个元素能形成的矩形的面积，要往它的左右相邻看（不能中断），如果有左、右大于它，就能和左、右构成矩形，也就是这个矩形的高是这个元素，宽是构成矩形的元素的个数

元素是now栈的栈顶，pass栈里存放的是判断过的元素，也就是正在判断的元素的右面的元素，而正在判断的元素左边的元素就是now里的

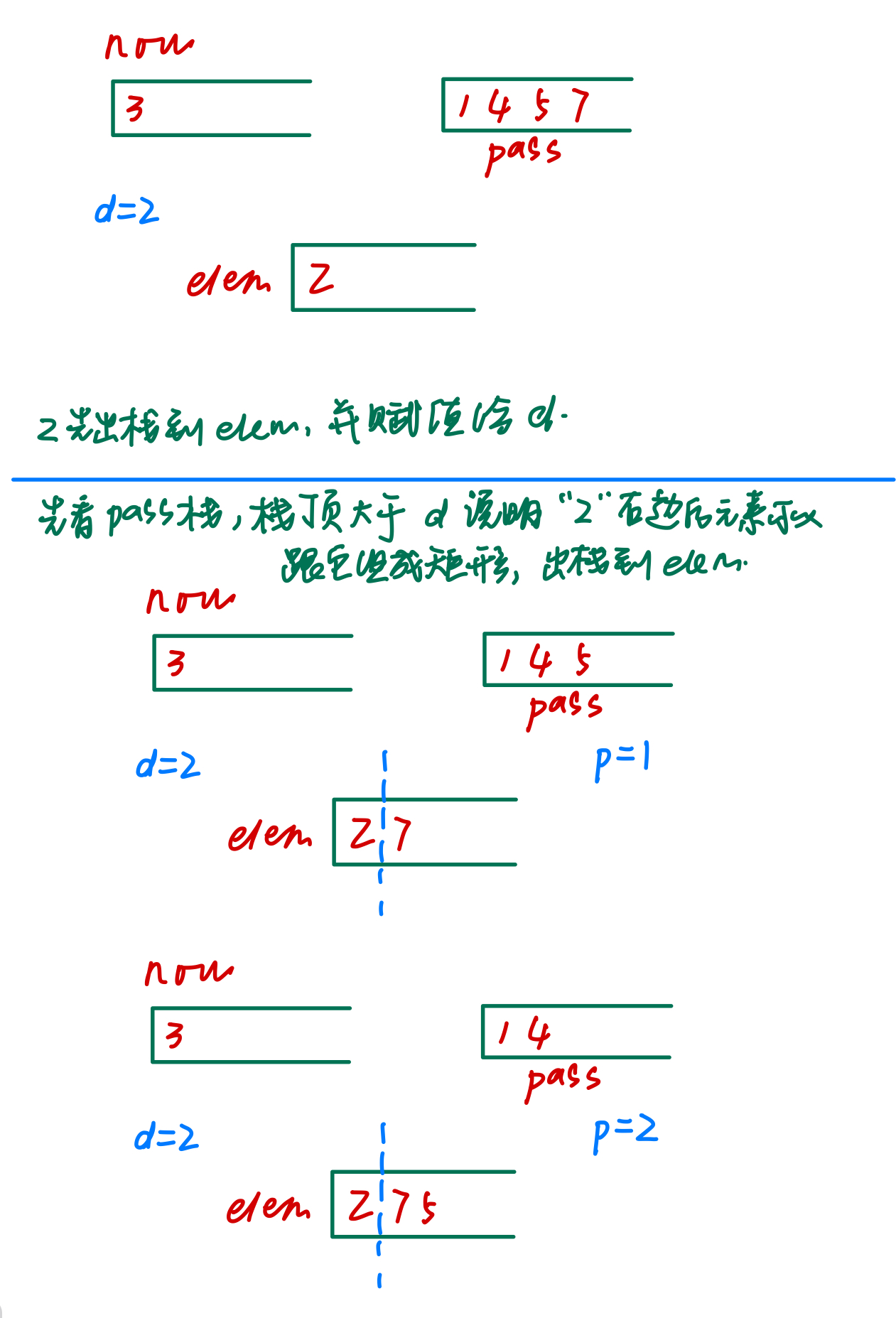
先将判断的元素出栈，赋值给d，并入栈到elem，elem是一个用来集合符合左右大于判断的元素的元素的栈，elem里的元素都是能构成矩形的元素

先判断 被判断的元素右面有没有可以和它组成矩形的元素，也就是从pass里找，如果栈顶大于，就出pass到elem中，再看pass的新栈顶，直到pass栈顶小于被判断的元素。pass每出一个元素到elem中，就用p计数，p++。p用来记录被判断的元素右面有几个可以和它组成矩形的元素。

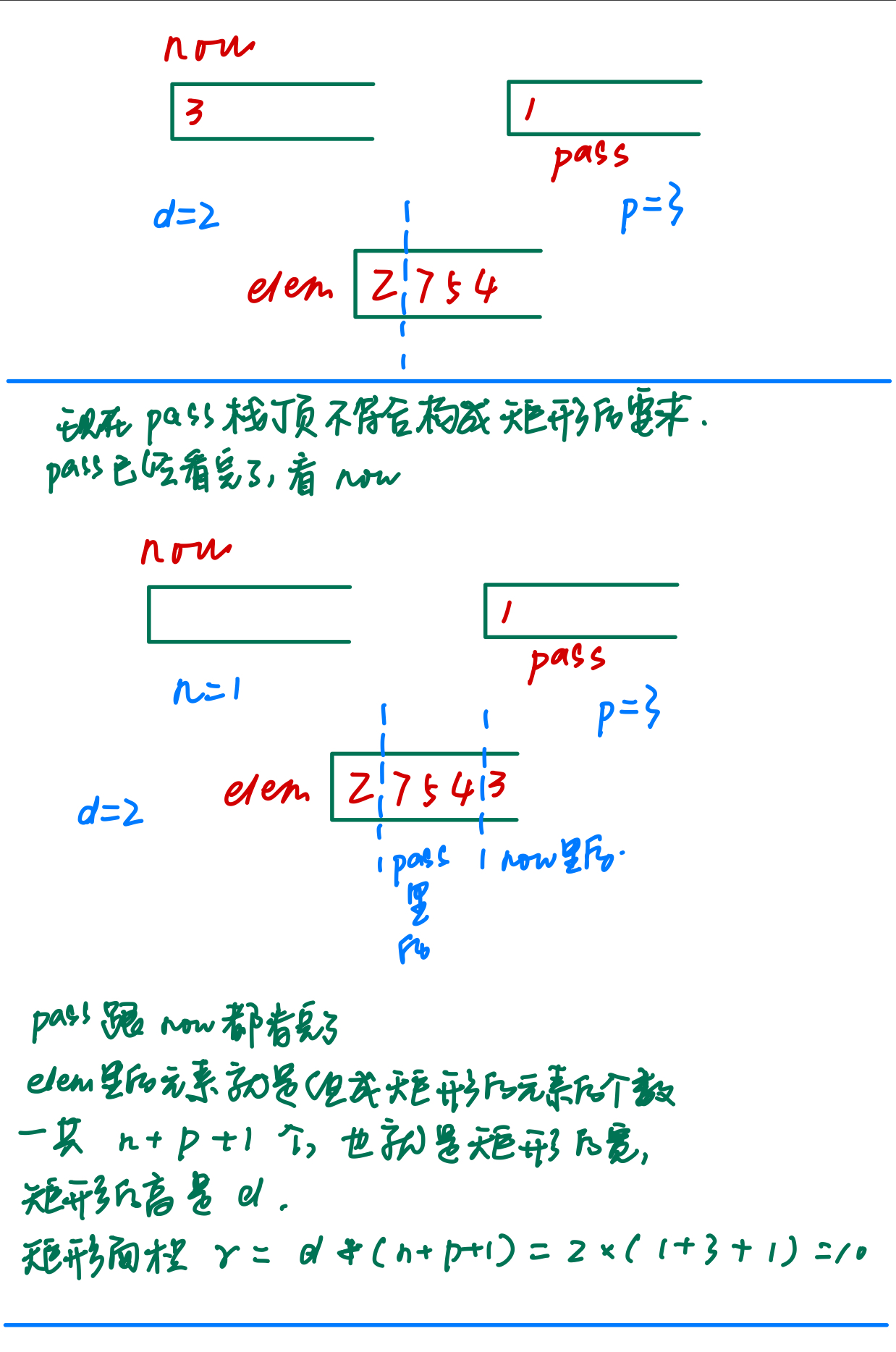
再看 被判断的元素左面，也就是从now里找，因为被判断的元素已经出now了，所以现在now里是新栈顶，如果now栈顶大于被判断的元素，就出now到elem，再看新栈顶，直到now栈顶小于被判断的元素。用n计数出now到elem的元素个数。

现在就可以计算当前被判断的元素能组成的矩形面积了：高（d） * 宽（p+n+1），其中1是被判断的元素自己，p+n+1就是组成矩形的元素的个数，也就是elem里元素的个数

因为进elem的顺序是：

d、p个pass栈的、n个now栈的

而now、pass栈进了elem还得出来，因为elem只是起统计作用的，不能破坏原来now和pass的内容

因为elem的元素还要回到now和pass里

now最后进的，就先出，进了n个，就每次出一个，n–，直到n=0，说明elem里now的元素都返回now了

elem里剩下的全部进pass就可以，因为elem栈底的d刚刚被判断过了，应该属于pass了，即元素出elem到pass直到elem空