数据结构_SinglyLinkedList单链表（C++实现

前言：此类笔记仅用于个人复习，内容主要在于记录和体现个人理解，详细还请结合bite课件、录播、板书和代码。

[toc]

前言&注意事项

  1. 单链表C++的实现分为了结点类和链表类两个类，十分明了，可读性很高，也很容易写，节点类负责单个节点的操作，链表负责链表整体的操作

  2. ==assert果然还是太暴力了，能不用就不用吧，但是一定要记住要判断 表指针 为空的情况==

    1. ==可以抛出异常信号 (建议用这个，因为运行错误的时候知道原因==
    2. ==可以直接返回==
    3. 判断指针head为空的方式
    1
    2
    3
    4
    5
    6
    7
    8
    9
    if(!head) // if(!head)等价于if(head==NULL),head==NULL是head为空时等式成立，值为真
      // head为空的话head就相当于0（假），非空就是真，所以当head为空的时候，!head就是真
      throw nullPointer();//这里使用了抛出异常信号的方式,而且抛出的是一个匿名对象(因为要的是它的类型，没必要给对象命名了)
                   
    //如果采用直接返回的方式
    if(!head)
        return;//直接返回的话，在有返回类型的函数里面可能会报错
                   
    //以上两者都可以终止函数，不过直接return只能用在无返回值函数上，return本质是终止函数运行并返回NULL

实现

SList.h

1
2
3
4
5
6
7
8
9
10
#include <iostream>

using namespace std;

class nullPointer
{
};//用作异常信号的类，遇到空指针时抛出，用于判断是否成功扩容以及头指针是否为空
class outofBound
{
}; //用作异常信号的类，用于判断是否越界
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
template <class elemType>
class sList; //类的向前说明，因为下面的node类将sList看作友元类，在此提前声明一下sList类的存在
//前面要声明参数模板，类后面不用跟参数模板

template <class elemType>
class node //节点类
{
	friend class sList<elemType>;//之后的sList中要用到node的私有成员data和next，只有将sList看作了友元类才行在sList中（属于node类外）访问node的私有成员
//友元类后面一定要跟参数模板

private:
	elemType data;
	node *next;

public:
	node() : next(NULL) {}					//默认构造函数
	node(const elemType &e, node *N = NULL) //含缺省参数的构造函数
	{
		data = e;
		next = N;
	}
};

==这里一定要注意为什么提前声明sList以及为什么node类将sList类看作友元类==

==还要注意==

==类的向前声明的时候类后面不加模板参数，但是前面一定要有参数模板的声明；==

==友元类后面一定要有模板参数==

==就按上面的写法==

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
template <class elemType>
class sList //单链表类
{
private:
	node<elemType> *head;

public:
	sList(); //构造函数，建立一个空链表

	bool sListempty() const; //判空，空则返回真，否则返回假

	// bool sListFull()const;//判满（额，我倒是想知道怎么判断是满的，没什么用这个

	int sListLength() const; //返回链表长度

	void sListPushBack(elemType &e); //尾插

	void sListPushHead(elemType &e); //头插

	void sListPopBack(); //尾删

	void sListPopHead(); //头删

	void sListInsert(int pos, elemType &e); //在pos位置插入e（在pos结点的前面插入e

	void sListErase(int pos); //删除pos结点

	elemType sListGet(int pos); //返回pos处的节点的值

	int sListFind(elemType &e); //返回值等于e的结点的序号，没有匹配的则返回0

	void sListRemove(int pos, elemType &e); //移除pos处的数据并赋值给e

	void sListReverse() const; //单链表元素就地逆置

	void sListClear(); //清空单链表，保留head结点，释放其余空间

	~sList(); //析构函数,销毁单链表，释放所有空间
};

SList.cpp

包含头文件以及构造函数的定义

1
2
3
4
5
6
7
#include "sList.h"

template <class elemType>
sList<elemType>::sList() //构造函数，建立一个空链表
{
	head = new node<elemType>(); //开辟一个结点对象空间（这里new的对象最后面这里加了括号，加不加括号的区别请看code日记）
}
1
2
3
4
5
6
7
8
template <class elemType>
bool sList<elemType>::sListempty() const //判空，空则返回真，否则返回假
{
	if(!head)
      throw nullPointer();

	return head->next == NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
template <class elemType>
int sList<elemType>::sListLength() const //返回链表长度
{
	if(!head)
      throw nullPointer();

	int size = 0;
	node<elemType> *p = head->next; //这里是让p=head->next这样可以统计有效节点的个数
	while (p)
	{
		size++;
		p = p->next;
	}
	return size;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
template <class elemType>
void sList<elemType>::sListPushBack(elemType &e) //尾插
{
	if(!head)
      throw nullPointer();

	node<elemType> *New, *p = head; //这里让p=head，因为有链表为空的情况

	New = new node<elemType>(e); //new了一个data初始化了的对象
	while (p->next)				 //找到最后一个节点
	{
		p = p->next;
	}
	p->next = New;
}
1
2
3
4
5
6
7
8
9
10
11
12
template <class elemType>
void sList<elemType>::sListPushHead(elemType &e) //头插
{
	if(!head)
      throw nullPointer();

	node<elemType> *New, *p = head->next;

	New = new node<elemType>(e);
	head->next = New;
	New->next = p;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
template <class elemType>
void sList<elemType>::sListPopBack() //尾删
{
	if(!head)
      throw nullPointer();

	node<elemType> *p = head;
	if (head->next == NULL)		  //如果链表是空的
		return;					  //直接返回上一级函数
	if (head->next->next == NULL) //如果只有一个有效节点,不用找尾
	{
		delete head->next;
		head->next = NULL;
	}
	else
	{
		while (p->next->next) //找尾
		{
			p = p->next;
		}
		delete p->next;
		p->next = NULL;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
template <class elemType>
void sList<elemType>::sListPopHead() //头删
{
	if(!head)
      throw nullPointer();

	node<elemType> *p = head->next;
	if (head->next == NULL) //如果链表是空的
		return;				//直接返回上一级函数
	else
	{
		head->next = p->next;
		delete p;
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
template <class elemType>
void sList<elemType>::sListInsert(int pos, elemType &e) //在pos位置插入e（在pos节点的前面插入e
{
	if(!head)
      throw nullPointer();

	if (pos < 1) //如果pos小于1则非法访问（越界
		throw outofBound();

	node<elemType> *p = head, *New;
	int j = 0;
	while (p && j < pos - 1) // p为空说明走到了链表的最后面，也就是NULL
	{
		j++;
		p = p->next;
	}

	if (!p)
		throw outofBound();
	// return;
	New = new node<elemType>(e, p->next);
	p->next = New;
}

​ p的位置是在pos位的前一个，数据插在pos的位置就是插在p的后面，如果p在尾节点，插入在p的后面是没问题的，如果p走到了节点的尾部也就是尾结点的next也就是NULL，那说明pos肯定是超出了范围，否则在此之间p就能走到pos的前一个位置而终止循环

​ 插入是可以尾插的，即pos的位置是在最后一个节点的后面，或者说NULL的前面,此时p在尾结点

​ while里面j的作用是判断有没有走到pos的位置之前，如果j=pos-1，说明p走到了pos的前一个位置

​ 如果数组长度为7，pos的位置是8，那么在p走到最后一个节点的时候，j=7，p就停止移动，此时相当于尾插

​ 如果数组的长度是7，pos的位置是9，那么在p走到最后一个节点的时候，j=7，p不为空，j<8，p继续后移到NULL，此时走了到链表的尽头，说明了链表长度不够，要插入的位置是在NULL还往后，这是非法访问

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
template <class elemType>
void sList<elemType>::sListErase(int pos) //删除pos节点
{
	if(!head)
      throw nullPointer();

	if (pos < 1)
		throw outofBound();

	node<elemType> *p = head;
	int j = 0;
	while (p->next && j < pos - 1) // p->next为空说明p走到了最后一个节点，如果走到了最后一个节点，说明pos的位置越界
	{
		j++;
		p = p->next;
	}

	if (!p->next)
		throw outofBound();
	node<elemType> *tmp = p->next; // p是pos的前一个节点
	p->next = tmp->next;
	delete tmp;
}

删除只能删除存在的节点，如果删除超过长度的节点就是非法的，所以pos只能访问存在的节点的位置，即在NULL之前，head之后

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
template <class elemType>
elemType sList<elemType>::sListGet(int pos) //返回pos处的节点的值
{
	if(!head)
      throw nullPointer();

	if (pos < 1)
		throw outofBound();

	int j = 0;
	node<elemType> *p = head;

	while (p->next && j < pos - 1)
	{
		j++;
		p = p->next;
	}

	if (!p->next)
		throw outofBound();
	return p->next->data;
}

也是只能访问存在的节点的位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
template <class elemType>
int sList<elemType>::sListFind(elemType &e) //返回值等于e的结点的序号，没有匹配的则返回0
{
	if(!head)
      throw nullPointer();

	int i = 1;

	node<elemType> *p = head->next;
	while (p)
	{
		if (p->data == e)
			return i;
		i++;
		p = p->next;
	}
	return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
template <class elemType>
void sList<elemType>::sListRemove(int pos, elemType &e) //移除pos处的数据并赋值给e
{
	if(!head)
      throw nullPointer();

	if (pos < 1)
		throw outofBound();

	node<elemType> *p = head;
	int j = 0;
	while (p->next && j < pos - 1)
	{
		j++;
		p = p->next;
	}

	if (!p->next)
		return;
	node<elemType> *tmp = p->next; // p是pos的前一个节点
	p->next = tmp->next;
	e = tmp->data; //将pos出的data赋值给引用e
	delete tmp;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
template <class elemType>
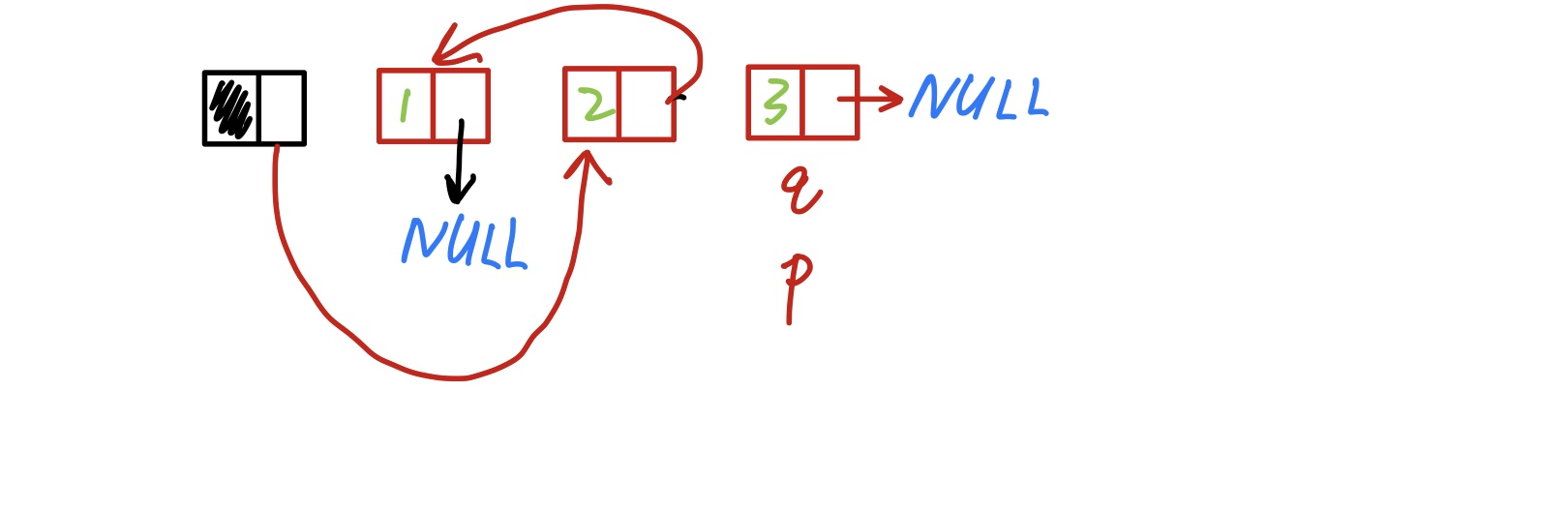
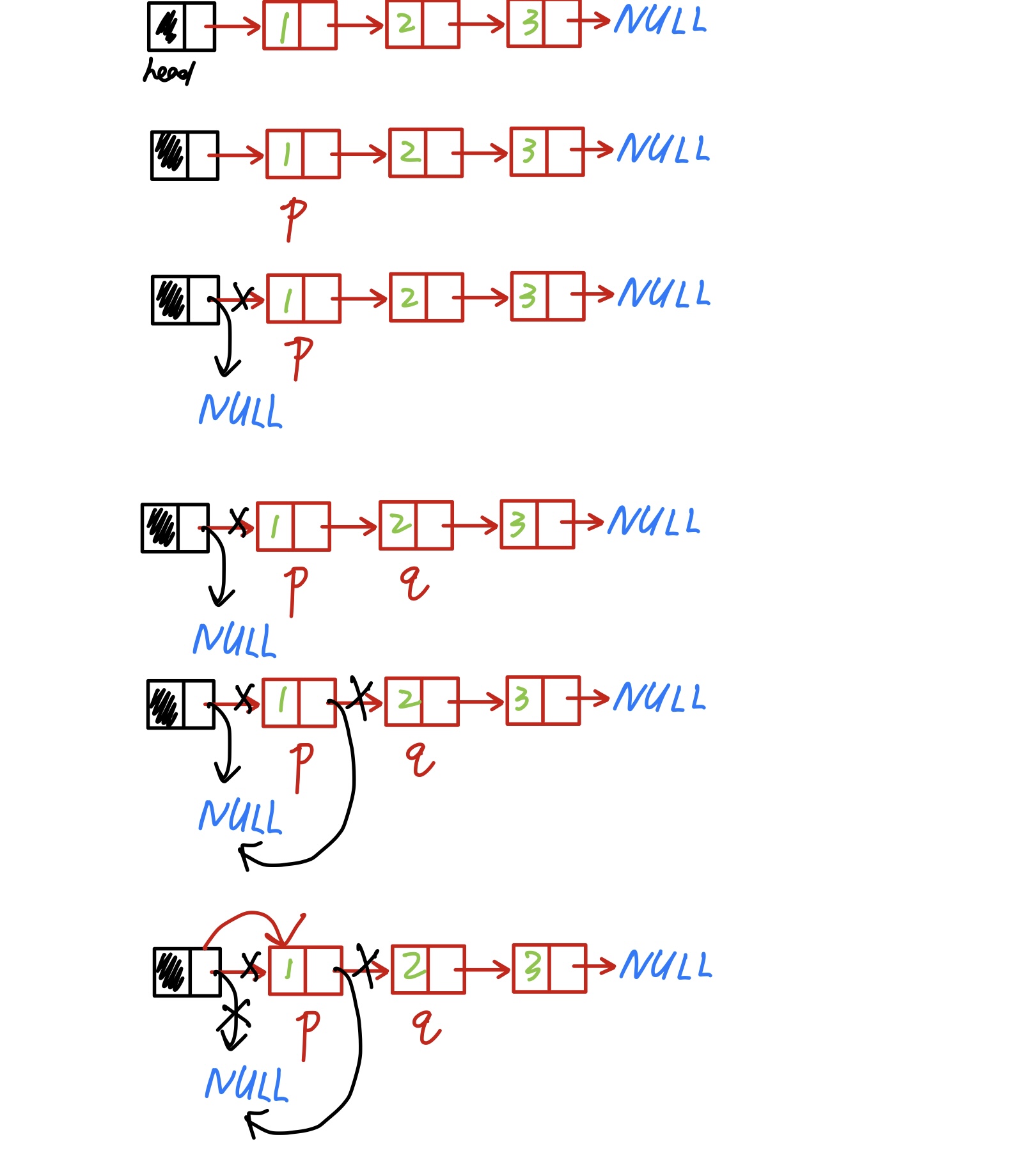
void sList<elemType>::sListReverse() const //单链表元素就地逆置 (这个比较重点
{
	if(!head)
      throw nullPointer();

	node<elemType> *p, *q; //兄弟协同
	p = head->next;
	head->next = NULL;
	while (p)
	{
		q = p->next;
		p->next = head->next;
		head->next = p; //首席插入
		p = q;
	}
}
IMG_0576 IMG_0577(20220913-081601) img
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
template <class elemType>
void sList<elemType>::sListClear() //清空单链表，保留head结点，释放其余空间
{
	if(!head)
      throw nullPointer();

	node<elemType> *p = head->next;

	while (p)
	{
		head->next = p->next;
		delete p;
		p = head->next;
	}
}
1
2
3
4
5
6
7
template <class elemType>
sList<elemType>::~sList() //析构函数,销毁单链表，释放所有空间
{
	sListClear();
	delete head;
	head == NULL;
}

总结

  1. 头部操作比尾部操作简单，因为尾部操作需要先找尾，找尾还要看有效节点是一个还是多个，一个的话就不用找，多个的话就要找
  2. 这里我犯了一个糊涂，混淆了一些东西，解释一下：
  1. new开辟动态内存之后返回的是地址
  2. 访问对象的成员的时候的格式是 对象.成员 ；使用指针来访问对象成员的时候是 对象指针->成员

这一点是因为，类和对象是一种特殊的结构体（自定义类型），结构体访问成员就是

结构体名.结构体成员

或者

结构体指针->结构体成员

  1. 匿名对象名后面无论加不加初始化参数都要有括号(C++异常处理有说明)
  2. 一定要写对单词！我写顺序表因为main写成mian找了很长时间的错误，写单链表因为friend写成了frind又找了很久错误

练习

1.约瑟夫环

n个人围成一个圈，从1、2、3开始报数。当报到m时，第m个人出列，并从原来的第m+1人重新开始1、2、3报数。如此循环，直到圈中只剩下一个人。这个圈称为约瑟夫环。试用单向循环链表实现该游戏，并输出最后剩下的那人的姓名。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<iostream>
#include<string.h>
using namespace std;

struct Node//单链表结点
{
	Node* next;
	string name;
};

struct Ring//约瑟夫环结构体（单向循环链表）
{
	Node* head;
	Node* tail;
};

void ThrowOut(Ring* ring, int n, int m)//用于让第m个人出列
{
	if (n < m)
		return;
	int j = 1;
	Node* temp=ring->head;
	Node* x=NULL;

	for (j; j < m-1; j++)
	{
		temp = temp->next;
	}

	//cout << temp->next->name << endl;//输出每次出列的人的名字
	x = temp->next;
	temp->next = temp->next->next;
	free(x);

	ring->tail = temp;
	ring->head = temp->next;

}

void ringGame(Ring* ring,int n)//约瑟夫环游戏实现函数
{
	while (ring->head == ring->tail)
	{
		int m;
		cout << "Please keynode the number you want to throw out" << endl;
		cin >> m;
		ThrowOut(ring, n, m);
	}
	cout <<"The last member's name is:  "<< ring->head->name << endl;
}

2.已知表头元素为c的单链表在内存中的存储状态如下表所示

地址
1000Ha1010H
1004Hb100CH
1008Hc1000H
100CHdNULL
1010He1004H
1014H

现将f存放于1014H处并插入到单链表中，若f在逻辑上位于a和e之间，则a，e，f的“链接地址”依次是什么？

原来逻辑上：c，a，e，b，d

现在逻辑上：c，a，f，e，b，d

则a的链接地址（后继指针）变成了f的地址，f的链接地址变成了e的，e的不变

即a->next=1014H, f->next=1010H, e->next=1004H

3.集合的并、差（不一定是有序的集合

利用链式结构分别实现集合运算
$$
C=A\cup B、C=A-B=A-A\cap B
$$
并分析其时间复杂度。要求运算结束后在内存中的A、B两个集合中的元素不变

思路：

求并集的时候，可以先将A、B简单相加得C，然后删除C中数据重复的结点

求差时候，以A为基础，A中的每个结点和B比较，A、B中有相同的就不插入C，把A中具有且B中没有的插入到C

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
#include<iostream>
using namespace std;

struct Node//单链表结点
{
	Node* next;
	int data;//方便起见就假设集合是一个数集吧~~
};

class CT//集合结构体,CT是collection的缩写
{
private:
	Node* head;
public:
	CT();
	void And(CT*, CT*);
	void Difference(CT*, CT*);
};

CT::CT()
{
	Node* C = new Node();
	head = C;
	C->next = NULL;
	C->data = 0;
}

void CT::And(CT* A, CT* B)//求并集:A+B-AB
{
	if (A == NULL || B == NULL )
		return;
	Node* a = A->head;
	Node* b = B->head;
	Node* c = head;

	while (a)
	{
		c->data = a->data;
		c->next = new Node();
		c = c->next;
		c->next = NULL;
		a = a->next;
	}
	while (b)
	{
		c->data = b->data;
		c->next = new Node();
		c = c->next;
		c->next = NULL;
		b = b->next;
	}
	c = head;
	while (c)
	{
		Node* x = c;
		Node* y = c->next;
		while (y)
		{
			if (c->data != y->data)
			{
				x = x->next;
				y = y->next;
			}
			else
			{
				x->next = y->next;
				delete(y);
				y = x->next;
			}
		}
		c = c->next;
	}
	
}

void CT::Difference(CT* A, CT* B)//求差集,遍历A中的每一个元素的时候遍历B中的每一个元素，有相同的就不加入到C，没有就加入到C
{
	Node* a = A->head;
	Node* c = head;

	if (A == NULL || B == NULL)
		return;

	while (a)
	{
		Node* b = B->head;
		while (b)
		{
			if (a->data == b->data)
			{
				break;
			}
			else
			{
				b = b->next;
			}
		}
		if (b == NULL)
		{
			c->data = a->data;
			c->next = new Node();
			c = c->next;
			c->next = NULL;
		}
		a = a->next;
	}
}

题目

==下面这些函数都是直接在上面👆写好的单链表头文件（sList.h）中作为了成员函数声明的，并在另一个文件中定义的==

当然也可以不用作为成员函数，而是重新写一个头文件和源文件，并在头文件中包含单链表的源文件来使用写好的单链表

但是因为题目大都是在现有链表的基础上进行操作，也就是对链表进行操作，不如直接写成链表的成员函数，直接在链表中调用更方便

1.求两个递增单链表的交、并、差集，并且要求结果也是递增的单链表

请用两种方案实现：一种是用原有空间，一种是用新的空间

用原有空间的话，就是以A为主链，将A作为结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
//交集 就是在A中只保留下来AB都有的
template<class elemType>
void sList<elemType>::intersection(sList& b)
{
	node<elemType> *i, *j;
	i = head;
	j = b.head->next;//这里有个彩蛋，类内访问外部同类对象的私有成员，这是合理的

	while (i->next && j)
	{
		if (i->next->data == j->data)
		{
			i = i->next;
			j = j->next;
		}
		else
		{
			if (i->next->data < j->data)
			{
				node<elemType> *k = i->next;
				i->next = i->next->next;
				delete (k);
				k = NULL;
			}
			else
				j = j->next;
		}
	}
	while (i->next)//如果主集合i指针之后不会空，应该清除多余的元素
	{
		node<elemType> *k = i->next;
		i->next = i->next->next;
		delete (k);
		k = NULL;
	}

	cout << "交集是" << endl;
	for (int x = 1; x <= sListLength(); x++)
	{
		cout << sListGet(x) << " ";
	}
	if (sListLength() == 0)
		cout << "空集" << endl;
	cout << endl;
}
//这里要注意，因为涉及删除，所以a中要用两个指针，或者指针指向被判断的元素的前一个，指针的next指向被判断的元素，为删除做准备
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
//并集就是把 B中有且A中没有的 给A
template<class elemType>
void sList<elemType>::unionSet(sList& b)
{
	node<elemType> *i, *j;
	i = head;
	j = b.head->next;

	while (i->next && j)
	{
		if (i->next->data == j->data)
		{
			i = i->next;
			j = j->next;
		}
		else
		{
			if (i->data < j->data)
			{
				if (i->next->data > j->data)
				{
					node<elemType> *k = new node<elemType>;//这里要注意，如果只是将j的结点给i的next，则结点之后所有都是j的结点了，因此只能新开一个结点并赋值
					k->next = i->next;
					k->data = j->data;
					i->next = k;
				}
				else
					i = i->next;
			}
			else
				j = j->next;
		}
	}
	if (j)//如果b没有走完，b中剩下的的元素一定都是比a中的大的，因此不用判断大小，全部给到a就可以，而且直接连接上结点就可以，不用新开结点再赋值
	{
		i->next = j;
	}

	cout << "并集是" << endl;
	for (int x = 1; x <= sListLength(); x++)
	{
		cout << sListGet(x) << " ";
	}
	if (sListLength() == 0)
		cout << "空集" << endl;
	cout << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
//差集就是保留A中有且B中没有的
template<class elemType>
void sList<elemType>::complementarySet(sList& b)
{
	node<elemType> *i, *j;
	i = head;
	j = b.head->next;

	while (i->next && j)
	{
		if (i->next->data == j->data)
		{
			node<elemType> *k = i->next;
			i->next = i->next->next;
			delete (k);
			k = NULL;
			j = j->next;
		}
		else
		{
			if (i->next->data < j->data)
			{
				i = i->next;
			}
			else
			{
				j = j->next;
			}
		}
	}

	cout << "差集是" << endl;
	for (int x = 1; x <= sListLength(); x++)
	{
		cout << sListGet(x) << " ";
	}
	if (sListLength() == 0)
		cout << "空集" << endl;
	cout << endl;
}

用申请新空间的方案：也就是用另外一个链表C作为结果链

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
//交集就是将A、B都有的才放入C
template<class elemType>
void sList<elemType>::intersection_new(sList& a, sList& b)
{
	node<int> *i = a.head->next;
	node<int> *j = b.head->next;

	while (i && j)
	{
		if (i->data == j->data)
		{
			sListPushBack(i->data);
			i = i->next;
			j = j->next;
		}
		else
		{
			if (i->data < j->data)
				i = i->next;
			else
				j = j->next;
		}
	}

	cout << "交集是" << endl;
	for (int x = 1; x <= sListLength(); x++)
	{
		cout << sListGet(x) << " ";
	}
	if (sListLength() == 0)
		cout << "空集" << endl;
	cout << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
//并集就是A有B没有，放入，B有A没有，放入，AB都有，放入
template<class elemType>
void sList<elemType>::unionSet_new(sList& a, sList& b)
{
	node<int> *i = a.head->next;
	node<int> *j = b.head->next;

	while (i && j)
	{
		if (i->data == j->data)
		{
			sListPushBack(i->data);
			i = i->next;
			j = j->next;
		}
		else
		{
			if (i->data < j->data)
			{
				sListPushBack(i->data);
				i = i->next;
			}
			else
			{
				sListPushBack(j->data);
				j = j->next;
			}
		}
	}
	while (i)
	{
		sListPushBack(i->data);
		i = i->next;
	}
	while (j)
	{
		sListPushBack(j->data);
		j = j->next;
	}

	cout << "并集是" << endl;
	for (int x = 1; x <= sListLength(); x++)
	{
		cout << sListGet(x) << " ";
	}
	if (sListLength() == 0)
		cout << "空集" << endl;
	cout << endl;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
//差集 A中有B中没有的放入C <或者简单一点，调用交集函数然后将A中的减去交集>
template<class elemType>
void sList<elemType>::complementarySet_new(sList& a, sList& b)
{
	sList<int> K;//先求出ab的交集K
	node<int> *m = a.head->next;
	node<int> *n = b.head->next;

	while (m && n)
	{
		if (m->data == n->data)
		{
			K.sListPushBack(m->data);
			m = m->next;
			n = n->next;
		}
		else
		{
			if (m->data < n->data)
				m = m->next;
			else
				n = n->next;
		}
	}

	node<int> *k = K.head->next;
	node<int> *i = a.head->next;
	while (i && k)
	{
		if (i->data != k->data)
		{
			sListPushBack(i->data);
			i = i->next;
		}
		else
		{
			i = i->next;
			k = k->next;
		}
	}
	while (i)
	{
		sListPushBack(i->data);
		i = i->next;
	}

	cout << "差集是" << endl;
	for (int x = 1; x <= sListLength(); x++)
	{
		cout << sListGet(x) << " ";
	}
	if (sListLength() == 0)
		cout << "空集" << endl;
	cout << endl;
}

2.已知线性表中的元素以值递增有序排列，并以单链表做存书结构。请写一种高效的算法，删除表中所有值大于mink且小于maxk的元素（如果表中有这样的元素），同时释放被删除的结点空间，并分析一下算法的时间复杂度

用双指针就可以解决，一个i在前，一个j在后

i先找到区间（大于mink小于maxk的区间）之前的第一个元素（也就是小于mink的元素里面的最后一个元素）（此时i->data<=mink , i->next->data>=mink)

然后j开始往后找到区间之后的第一个元素(也就是j一直往后，直到j->data>=mark)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
template <class elemType>
void sList<elemType>::interval(int mink, int maxk)
{
    node<int> *i, *j;
    j = i = head->next;

    while (i->next)
    {
        if (i->data <= mink && i->next->data <= mink)
            i = i->next;
        else
            break;
    }
    j = i;
    while (j->next)
    {
        if (j->data < maxk )
            j = j->next;
        else
            break;
    }
    while (i->next != j)
    {
        node<int> *k = i->next;
        i->next = i->next->next;
        delete k;
        k = NULL;
    }
}

结束

That’s all, thanks for reading!💐